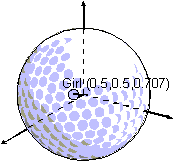
Eliasmith, C. (1997) Structure without symbols: Providing a distributed account of high-level cognition. Southern Society for Philosophy and Psychology. Conference March, 1997.
Philosophy-Neuroscience-Psychology Program,
Department of Philosophy, Washington University in St. Louis,
Campus Box 1073, One Brookings Drive, St. Louis, MO 63130-4899,
chris@twinearth.wustl.edu
There has been a long-standing debate between symbolicists and connectionists concerning the nature of representation used by human cognizers. In general, symbolicist commitments have allowed them to provide superior models of high-level cognitive function. In contrast, connectionist distributed representations are preferred for providing a description of low-level cognition. The development of Holographic Reduced Representations (HRRs) has opened the possibility of one representational medium unifying both low-level and high-level descriptions of cognition. This paper describes the relative strengths and weaknesses of symbolic and distributed representations. HRRs are shown to capture the important strengths of both types of representation. These properties of HRRs allow a rebuttal of Fodor and McLaughlin's (1990) criticism that distributed representations are not adequately structure sensitive to provide a full account of human cognition.
The earliest computational cognitive models were typically symbolic (see Newell, 1990). Commonly, such models employed logic-like rules and manipulated discrete symbols to mimic human cognitive capacities. This symbolicist tradition continues, and has had much success modeling high-level cognitive tasks such as planning, skill acquisition, analogical reasoning, problem solving, logical reasoning, elementary sentence verification and verbal recognition and recall (Newell, 1990; Falkenhainer et. al., 1989).
More recently, connectionism has provided another means of modeling cognitive function. These models can be distinguished from symbolicist models on the basis of a commitment to a different type of representation. Where symbolicists employ discrete symbolic representation, connectionists are committed to a distributed form of representation1. The greatest successes of connectionist models have been on low-level cognitive tasks such as categorization, recognition, and simple learning (Rumelhart and McClelland, 1986; Churchland, 1989).
Critics of connectionism often contend that these models, though impressive in some ways, have little to do with high-level human cognition. The models typically lack the right properties; namely, those exhibited by users of natural language (Fodor and Pylyshyn, 1988; Fodor and McLaughlin, 1990; c. f. Bechtel, 1995). Conversely, critics of symbolicism claim that such models do not seriously consider the types of processing taking place in the brain. The result is the inability of symbolicist models to account for developmental phenomena, the plasticity of the brain, and many low-level cognitive tasks (Churchland and Sejnowski, 1992; Churchland, 1989).
Until recently, connectionist distributed representations have been unable to provide an effective means of capturing the complex embedded structure necessary for many high-level cognitive tasks. Though there is general agreement among both connectionists and neuroscientists that representation in the brain is distributed (see footnote 1), there has been no way of providing distributed models of structure-dependent tasks such as language processing, planning, or analogy (Hinton, 1986; Miikkulainen and Dyer, 1988; Smolensky, 1988; Churchland, 1989; Churchland and Sejnowski, 1992). Fodor and McLauglin (1990) provide a general critique of distributed models inspired by these traditional difficulties of connectionism. They intend to show that distributed representations are not amenable to high-level cognition.
In order for us to provide models which can explain phenomena from the lowest to the highest levels of human cognition its seems we have two choices:
There are a number of reasons why distributed representations are more likely to provide a unifying representational medium than symbolic representations. First, distributed representations can be learned from the environment of the cognizer (Hinton, 1986). Second, distributed representations are equally applicable to all modes of perception (i.e. vision, hearing, olfaction, etc.). Third, there have been recent developments in distributed representations that provide an effect means of capturing embedded structure (Smolensky, 1990; Plate, 1993). And fourth, distributed representations are undeniably present in the brain and provide a degree of neurological realism not found in symbolic models (Churchland and Sejnowski, 1992; Churchland, 1995).
In this paper I will develop a version of the second option. Section 2 presents a general explanation of distributed representation. Section 3 describes holographic reduced representations (HRRs) which are a form of distributed representations that effectively capture structure. Finally, section 4 discusses how these representations overcome the criticisms of Fodor and McLaughlin (1990) of connectionist distributed representations. Fodor and McLaughlin's failure is an indication of the ability of such representations to an play important role in both low-level and high-level cognitive modeling.
The concept of distributed representation is a product of joint developments in the neurosciences and in connectionist work on recognition tasks (Churchland and Sejnowski, 1992). To introduce distributed representations as employed by connectionists, it is helpful to contrast them with symbolic representations of symbolicism.
A symbol, such as a word or a number, is an everyday occurrence for most of us. Of course, symbols are not restricted to being words or numbers, but this is by far their most common guise in symbolicist models. From computational, psychological, and neurological standpoints, there are a number of shortcomings in using purely symbolic representation in modeling human behavior. I will briefly examine three of the more important limitations of symbolic representation that serve to distinguish them from distributed representations.
First, symbolic representations are strongly propositional. Thus, when this method of representation is used in non-language based tasks such as image processing it becomes extremely difficult to explain many psychological findings (Kosslyn, 1994). Similarly, taste, sound, touch, and smell are awkward to handle with symbolic representations. In contrast, distributed representations are equally well suited to all modes of perception.
Second, symbolic representations are 'all-or-none'; this property is referred to as brittleness. There is no such thing as the degradation of a symbolic representation, it is either there (whole), or it is not there (broken). The brittleness of symbolic representations is highly psychologically unrealistic. People often exhibit behavior that indicates partial retrieval of representations, as exemplified by 'tip-of-the-brain' recall, prosopagnosia (loss of face recognition), and image completion. Furthermore, minor damage to a symbolic conceptual network causes loss of entire concepts, whereas a distributed network loses accuracy, as people do, not entire concepts (Churchland and Sejnowski, 1992).
Third, symbolic representations are not, in themselves, statistically sensitive (Smolensky, 1995). In other words, they are not constructed based on statistical regularities found in the environment. Therefore, symbolic representations are not amenable to modeling low-level perception. This sort of low-level perceptual learning seems to be common to all animals, and is an important part of human development. It is the case, however, that though symbolic representations are not statistically sensitive, they are superbly structurally sensitive. To many, this had seemed a reasonable trade-off in light of structurally insensitive alternatives. However, with the more recent development of distributed representations that exhibit both structural and statistical sensitivity, this trade-off is no longer easily justifiable.
Because of the limitations of symbolic representations, many cognitive scientists have searched for, and found an alternative; distributed representations. Distributed representations are considerably less common in everyday life. As an explanatory aid, consider the following analogy (to which we will return in section 3): imagine all of your concepts are mapped to the surface of a sphere - a conceptual golf ball, if you will (figure 1). Each concept is nestled in a dimple on surface of the golf ball. The more similar two concepts are, the closer together they will be on the surface of the golf ball. Also, the distance from the center of the golf ball to any particular dimple (i.e. concept) is approximately the same (one golf ball radius).
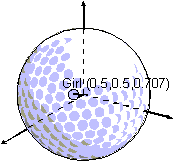
The easiest way to identify the position of a concept on the surface of the ball is to provide its coordinates. These coordinates are in the units of 'golf ball radii' and are continuous real values. Thus, in figure 1, 'girl' has coordinates (0.5, 0.5, 0.707). Such a set of coordinates is commonly referred to as a vector. This representation of 'girl' is a distributed representation, because the 'girl' dimple can only be located through knowing all three values. Thus, the concept of 'girl' is shared, or distributed, across the three dimensions of the golf ball's coordinate system.
Notably, a dimple on a golf ball is not a single point in space, rather it is a collection of points which are in proximity on the surface of a sphere. This makes the dimple particularly appealing as an analogy for our concepts for the following reasons:
We will revisit the conceptual golf ball in our examination of the particular type of distributed representations which allow us to successfully capture structure (section 3).
Earlier, I noted that much of the reason researchers were motivated to look for alternate forms of representation was due to the failings of symbolic representations. In particular, the propositional, brittle, and statistically insensitive nature of symbolic representations were shown to be problematic. Distributed representations do not fall prey to these short-comings. Rather, distributed representations:
Furthermore, distributed representations have a number of properties which lend significant psychological and neurological plausibility to models employing them. Most often, distributed representations:
These powerful properties, coupled with the ability of distributed representations to avoid short-comings of symbolic representation, provide a solid foundation for realistic computational models of human cognition. Armed with the strengths of distributed representations and our conceptual golf ball analogy, we will now examine the type of representations that can provide structure without symbols.
Holographic reduced representations or HRRs are structurally sensitive, but distributed vector representations (Plate, 1994). These representations are constructed, or encoded, using a form of vector multiplication called circular convolution and are related to the better-known tensor products of Smolensky (Smolensky, 1990). Decoding of HRRs is performed using the approximate inverse of circular convolution, an operation called correlation (see appendix A for the algebraic details of these operations).
The HRR representations are "holographic" because the encoding and decoding operations (i.e. convolution and correlation) used to manipulate these complex distributed representations are the same as those which underlie explanations of holography (Borsellino and Poggio, 1973). The convolution of two HRRs creates a third unique HRR which encodes the information present in the two previous HRRs. Importantly, this new HRR is not similar to either of its components, though the components may be retrieved through decoding the new HRR with the correlation operator. These operations are easiest to understand through a simple illustration. Let A, B and C be distributed HRR vectors (i.e. as per the concept 'girl' presented in section 2). If C = A ƒ* B (read: C equals A convolved with B) then, C # A B (read: C correlated with A approximately equals B) and C # B A (see figure 2).

Figure 2. HRR operations depicted on the conceptual golf ball. Vector C is the circular convolution of vectors A and B. Vector D is the normalized superposition of A and B.
Along with convolution another operation, superposition, can be used to combine two HRR vectors. Superposition of two vectors simply results in their sum, and is written: D = A + B (see figure 2). Superimposing two vectors results in a vector which is very similar to the original two vectors but cannot provide a perfect reconstruction of the original vectors. This contrasts with convolution, in which the resulting vector is nothing like the original two vectors; in fact, the expected similarity of either of the original vectors to their convolution is zero (Plate, 1994, p. 57). In both cases, some of the information in the original HRR vectors is lost in their combination. Hence, HRRs are considered 'reduced' representations. Upon encoding a new representation from a number of others (e.g. constructing the representation for a particular 'girl' from 'female', 'small', 'human', etc.), the new representation does not contain all of the information present prior to encoding. In other words, the new representation is noisy. Nevertheless, these representations are extremely effective at capturing complex relational information. Furthermore, the noise occurring in HRRs seems to have a neurological counterpart (Andersen, personal comment).
When decoding an HRR vector the resultant vector must be recognized even though it is not expected to be identical to the vector that was encoded. The process of recognizing a vector is accomplished through use of another operator called the dot product and represented as 'ï'. The dot product of two vectors is the sum of the product of each of the corresponding elements of the vectors. For normalized vectors, the resulting scalar is equivalent to the length of one of the vectors projected on to the other. This relative length value can be used as a measure of the vectors' similarity. Because all of our conceptual vectors are normalized to one golf ball radius, we can use the dot product operation to determine the similarity of any two vectors.
A number of properties of HRRs make them promising candidates for modeling human cognition. First, HRRs are distributed representations. This means that they have all of the benefits associated with distributed representations. Therefore, HRRs (see section 2): 1. Are sensitive to statistical input; 2. Provide cross-modal representations; 3. Degrade gracefully; 4. Represent concepts continuously; 5. Can be processed in parallel, and; 6. Are subject to the many learning algorithms already developed.
Second, HRRs accommodate arbitrary variable binding through the use of convolution. Third, HRRs can effectively capture embedded structure (Plate, 1994; Eliasmith and Thagard, forthcoming). Fourth, unlike tensor products, and most other distributed representations which use vector multiplication, HRRs are fixed dimension vectors. Thus, convolving two three-dimensional vectors results in another three-dimensional vector - not a six- or nine-dimensional vector. Consequently, HRRs are not subject to an explosion in the size of representations as the structures represented become more complex. This property also allows HRRs of various structural depths to be easily comparable to each other with out "padding" the representation, as is necessary with tensor products. Fifth and finally, convolution can be implemented by a recurrent connectionist network (Plate, 1993). The potential for implementation in a recurrent network supports the neurological plausibility of HRRs. Though the extent of neurological realism of any such artificial neural networks may be disputed, it is indisputable that they are more neurologically realistic than either localist connectionist or symbolic models (Smolensky, 1995).
Most important to modeling high-level cognition are the structural properties. The ability of HRRs to accommodate arbitrary variable bindings and embedded structure will allow distributed models to handle structures as complex those in symbolicist systems. As well, HRRs maintain the traditional strengths of distributed representations and can be applied to modeling low-level cognition.
Providing a form of distributed representation which can be used to model higher cognitive function provides support to the contentious claim that connectionist ideas will scale to the complexity of high-level human cognition; a feat some thought may not be possible (Gentner and Markman, 1993). More particularly, the claims by Fodor and Pylyshyn (1988) and more recently Fodor and McLaughlin (1990) that connectionist systems can not exhibit certain characteristics necessary for modeling human cognition can be directly challenged.
For Fodor and McLaughlin, the most obvious failing of distributed representations, including tensor products (and thus presumably HRRs), is a lack of systematicity. They characterize systematicity as follows (Fodor and McLaughlin, 1990, p. 184):
[A]s a matter of psychological law, an organism is able to be in one of the states belonging to the family [of semantically related mental states] only if it is able to be in many of the others…[for example] You don't find organisms that can think the thought that the girl loves John but can't think the thought that John loves the girl.
A system employing HRRs can satisfy this definition of systematicity. In representing structure, an HRR representation consists in a series of convolutions and superpositions. For example, to represent the sentence 'John loves the girl' we would perform the following operations:
S1 = relation*love + agent*John + patient*girl
Where each of 'relation', 'love', 'agent', 'john', 'patient', and 'girl' are HRRs. The resulting sentence vector, S1, will successfully encode the example proposition proposed by Fodor and McLauglin. Furthermore, constructing the complementary sentence 'The girl loves John' uses exactly those HRRs needed for S1, i.e.:
S2 = relation*love + agent*girl + patient*John
Thus, an HRR system capable of encoding the first sentence (S1) can necessarily encode the second (S2). In other words, an HRR system is systematic in just the right way. Also note that vectors S1 and S2, if compared to one another would be quite similar, as expected, but distinct nonetheless. If sentence S1 is queried as to the agent of the sentence (by performing the operation S1#agent), the result indicates that the agent is 'John'. Conversely, if S2 is queried as to the agent (S2#agent), the result is the vector for 'girl'.
Accounting for systematicity with such little effort naturally raises the concern that this sort of HRR system is simply a new implementation of the 'classical' (i.e. Fodor and McLaughlin's) solution. This, however, is clearly not the case. Fodor and McLaughlin provide the following definition of a 'classical constituent' (ibid., p. 186):
[F]or a pair of expression types E1, E2, the first is a Classical constituent of the second only if the first is tokened whenever the second is tokened.
With HRRs it is not the case that when the sentence S1 is tokened, any of the components of that sentence are tokened. We can easily combine sentences S1 and S2 to form the following sentence, S3:
S3 = relation*cause + agent*S1 + patient *S2
In tokening S1 and S2 to form this sentence, we in no way tokened the vector 'John'. Rather, a vector which, when operated upon by a given operator, produces the vector 'John' was tokened. Thus, constituents of S1 and S2 are 'non-classical' in the sense provided by Fodor and McLaughlin.
Fodor and McLaughlin would likely agree, but they would conclude that therefore, HRRs are not systematic. In the abstract of their 1990 paper, they claim to show (ibid., p. 183, my italics):
[Such] representations fail to explain systematicity because they fail to exhibit the sort of constituents that can provide domains for structure sensitive mental processes.
While it is true that the constituents of HRR representations are non-classical, it is not true that this sort of constituent is necessary for providing structure sensitive processes. Eliasmith and Thagard (forthcoming) provide a detailed model of analogical reasoning in which HRRs are used as the representational medium. This model, called Drama, is as structurally sensitive as any competing symbolic models (see Falkenhainer et. al., 1989; Mitchell, 1993). The relations between and within sentences describing given analogies is correctly captured with HRRs. The domain of human analogy making is one of the most structurally demanding of those tackled by computational models of cognition (Gentner and Markman, 1993). If it were truly the case, as Fodor and McLauglin claim, that representational systems employing HRRs were necessarily structurally insensitive, it would be impossible to provide a model of analogy. There can be little stronger proof that HRR systems can indeed be systematic than the existence of highly structure sensitive HRR models like Drama.
In sum, HRR systems meet Fodor and McLaughlin's (1990) criteria for being systematic. However, HRR systems do not meet their criteria for using classical constituents and are thus not an implementation of the classical solution to the systematicity problem. Therefore, the structural sensitivity necessary for systematicity does not have to be provided by symbolic models, as is demonstrated in the Drama model of analogy.
Holographic reduced representations (HRRs) provide an important new means of bridging the gap between low-level and high-level cognitive models. Because HRRs are distributed representations, they have all of the properties of this form of representation which make them ideal for modeling low-level cognitive processes. With the four operators of convolution, correlation, superposition, and the dot product, distributed vectors can be used to effectively capture structural relations. Each of these operators is naturally implemented in artificial neural networks and thus there is no loss of neurological plausibility in their usage (Plate, 1994).
The symbolicist monopoly of high-level cognitive models can be seriously challenged by distributed systems which employ HRRs. The attempt of Fodor and McLaughlin (1990) to show that such representations were unable to capture structure effectively failed in both theory and in practice (Eliasmith and Thagard, forthcoming). The potential of HRRs remains to be seen, but by all indications, this representational medium can provide a means of unifying low-level and high-level models of human cognitive processes.
* Thanks to Paul Thagard, Cameron Shelley, Poco deNada, and to Tony Plate for his insights into the workings of HRRs. This research was supported in part by the Natural Sciences and Engineering Research Council of Canada.
Bechtel, W. (1995). Connectionism. A companion to the philosophy of mind. Cambridge, MA, Blackwell.
Borsellino, A. and T. Poggio (1973). 'Convolution and correlation algebras.' Kybernetik 13: 113-122.
Churchland, P. (1989). A neurocomputational perspective. Cambridge, MA, MIT Press.
Churchland, P. M. (1995). Machine stereopsis: A feedforward network for fast stereo vision with movable fusion plane. Android Epistemology. Menlo Park, MIT Press.
Churchland, P. S. and T. Sejnowski (1992). The computational brain. Cambridge, MA, MIT Press.
Clark, A. and J. Toribio (1994). 'Doing without representing?' Sythese 101: 401-431.
Eliasmith, C. (in press). "The third contender: A critical examination of the dynamicist theory of cognition." Philosophical Psychology.
Eliasmith, C. and P. Thagard (forthcoming) "Integrating structure and meaning: A distributed model of analogical mapping."
Falkenhainer, B., K. D. Forbus, and D. Gentner (1989). 'The structure-mapping engine: Algorithms and examples.' Artificial Intelligence 41: 1-63.
Fodor, J. and B. McLaughlin (1990). 'Connectionism and the problem of systematicity: Why Smolensky's solution doesn't work.' Cognition 35: 183-204.
Fodor, J. and Z. Pylyshyn (1988). 'Connectionism and cognitive architecture: A critical analysis.' Cognition 28: 3-71.
Gentner, D. and A. B. Markman (1993). Analogy - watershed or Waterloo? Structural alignment and the development of connectionist models of analogy. Advances in neural information processing systems. San Mateo, CA, Morgan Kaufmann.
Gorman, R. P. and T. J. Sejnowski (1988). 'Analysis of hidden units in a layered network trained to classify sonar targets.' Neural Networks 1: 75-89.
Harnad, S. (1992). Connecting object to symbol in modelling cognition. Connectionism in Context. London, Springer-Verlag.
Hinton, G. E. (1986). Learning distributed representations of concepts. Eighth Conference of the Cognitive Science Society, Lawrence Erlbaum Associates.
Hofstadter, D. (1995). A review of mental leaps: analogy in creative thought. AI Magazine. 16: 75-80.
Holyoak, K. and P. Thagard (1995). Mental leaps: Analogy in creative thought. Cambridge, MA, MIT Press.
Holyoak, K. J. and P. Thagard (1989). 'Analogical mapping by constraint satisfaction.' Cognitive Science 13: 295-355.
Kosslyn, S. (1994). Image and brain: The resolution of the imagery debate. Cambridge, MA, The MIT Press.
Lazzaro, J. and C. Mead (1989). 'A silicon model of auditory localization.' Neural Computation 1: 47-57.
Le Cun, Y., B. Boser, J. Denker, D. Henderson, R. Howard, W. Hubbard, and L. Jackel (1990). Handwritten digit recognition witha back-propagation network. Advances in neural information processing systems. San Mateo, Morgan Kaufmann. 396-404.
Legendre, G., Y. Miyata, and P. Smolensky (1994). Principles for an integrated connectionist/symbolic theory of higher cogntion. Hillsdale, NJ, Lawrence Erlbaum Associates.
Miikkulainen, R. and M. G. Dyer (1988). Encoding input/output representations in connectionist cognitive systems. Connectionists models summer school, San Mateo, Morgan Kaufmann Publishers.
Mitchell, M. (1993). Analogy-making as perception. Cambridge, Massachusetts, MIT Press.
Plate, T. A. (1993). Holographic recurrent networks. Advances in neural information processing systems. San Mateo, Morgan Kaufmann. 34-41.
Plate, T. A. (1994). Distributed representations and nested compositional structure. University of Toronto.
Qian, N. and T. J. Sejnowski (1988). Learning to solve random-dot seterograms of dense and transparent surfaces with recurrent backpropagation. Connectionist Models Summer School, San Mateo, Morgan Kaufmann Publishers.
Raeburn, P. (1993). Reverse engineering the human brain. Technology Review.
Rumelhart, D., P. Smolensky, G. Hinton, and J. McClelland (1986). Schemata and sequential thought processes in PDP models. Parallel distributed processing: Explorations in the microstructure of cognition. Cambridge MA, MIT Press/Bradford Books. 7-57.
Rumelhart, D. E. and J. L. McClelland, Ed. (1986). Parallel distributed processing: Explorations in the microstructure of cognition. Cambridge MA, MIT Press/Bradford Books.
Sarle, W. S. (1994). Neural networks and statistical models. 19th Annual SAS Users Group International Conference.
Skarda, C. A. and W. J. Freeman (1987). 'How brains make chaos in order to make sense of the world.' Behavioral and Brain Sciences 10: 161-195.
Smolensky, P. (1988). 'On the proper treatment of connectionism.' Behavioral and Brain Sciences 11(1): 1-23.
Smolensky, P. (1990). 'Tensor product variable binding and the representation of symbolic structures in connectionist systems.' Artificial Intelligence 46: 159-217.
Smolensky, P. (1995). Computational models of mind. A companion to the philosophy of mind. Cambridge, MA, Blackwell.
Consider a set E of elements which are holographic reduced representations (HRRs). A member of E is an n-dimensional vector whose contents may represent an image, a proposition, a concept, etc. The prima facie similarity of two vectors is captured by their dot product. The operations necessary to encode and decode HRRs can be understood as follows:
Let be the space of item vectors
in n-dimensions, and let
be the space of
stored vectors in n-dimensions.
Let
be the encoding operation (circular convolution),
be the decoding operation (circular correlation), and
be the superposition operation (addition). These three operations make it possible to store any relations necessary for generating the network of relations amongst elements of E.
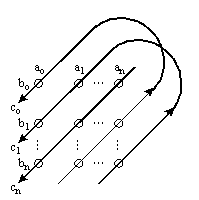
More precisely, the circular convolution operation ƒ is often referred to simply as convolution and consists of the following operations for c = a ƒ b where a, b, and c are n-dimensional vectors:
co = aobo + anb1 + an-1b2 + ... + a1bn
c1 = an-1bo + an-2b1 + ... + anbn
cn = anbo + an-1b1 + ... + aobn
or
for j=0 to n-1 (subscripts
are modulo-n)
This operation can be represented as:
Similarly, the circular correlation operation # is often referred to simply as correlation and consists of the following operations for d = a # c:
do = aoco + a1c1 + ... + ancn
d1 = anco + aoc1 + ... + an-1cn
dn = a1co + anc1 + ... + aocn
or
for j=0 to n-1 (subscripts
are modulo-n)
This operation can be represented as:

Notably, the correlation of two vectors a # c can be written as a* ƒ c where a* is the approximate inverse of a which is defined as:
Let
a = {ao, a1, ..., an}
then
a* = {ao, an, ..., a1}
Though the exact inverse, a-1, could be used to decode a ƒ c exactly, this process results in a lower signal-to-noise ratio in the retrieved vectors in most instances.