Is the Brain Analog or Digital?
The Solution and Its Consequences for Cognitive Science*
1. Introduction and Preliminaries
The concepts of continuity and discreteness have perplexed philosophers since the time of Parmenides. Kant (1783/1997) has put the problem as follows:
It will always remain a remarkable phenomenon in the history of philosophy, that there was a time, when even mathematicians, who at the same time were philosophers, began to doubt, not of the accuracy of their geometrical propositions so far as they concerned space, but of their objective validity and the applicability of this concept itself, and of all its corollaries, to nature. They showed much concern whether a line in nature might not consist of physical points, and consequently that true space in the object might consist of simple [discrete] parts, while the space which the geometer has in his mind [being continuous] cannot be such.
Kant recognizes not only the distinction between continuity and discreteness but more importantly, the problem of relating these concepts to nature; that is, to real physical systems. More recently, cognitive science has posed the related question: Does the brain function in an analog or digital manner? Or, more precisely, is the brain digital or analog at the level of description amenable to explaining cognitive phenomena? The answer for many is obvious, it just happens that they disagree on what the answer is. The concern of cognitive science with this distinction has been evident since its inception. Cyberneticists including Von Neumann, McCulloch, Pitts, Wiener, and Freemont-Smith hotly debated the analog/discrete distinction as early as 1951 (Gerard, 1951).[1] Current researchers, including Churchland (1995), Fodor (1983), Newell (1990), van Gelder (1995), and Smolensky (1988) have emphasized the importance of a commitment to one or the other of these views of the brain. A definitive answer to the question “Is the brain analog or digital?” should prove invaluable in evaluating the available theories in cognitive science.
I believe such an answer can be provided. In this paper, I argue that there is strong evidence that the brain is digital. Before explaining the reasons for this conclusion I characterize the debate, sketching the various reasons for and against both the digital/discrete and analog/continuous views. This will provide background against which we can consider a definition of the continuity or discreteness of any given physical system. This definition relies on a distinction between types of continuity or discreteness suggested by van Gelder (in press). He has suggested that there is an important distinction to be made between continuity (or discreteness) of state and continuity (or discreteness) in time. Any adequate solution to the continuity debate needs to address both types of continuity. Definition in hand, I detail a solution to the continuity/discreteness debate, concluding that the brain is discrete at the level of analysis necessary for explaining cognition. This solution provides a basis for a brief analysis of the various cognitive theories espoused in cognitive science, including symbolicism (Newell 1990), connectionism (Churchland and Sejnowski 1992), and dynamicism (van Gelder 1995).
One brief terminological clarification needs to be made before continuing. Most current discussions are consistent in regards to the lack of a distinction between ‘analog and continuous’ and ‘digital and discrete’ (see Lewis 1971 for a counter instance). Consider Suber’s (1988) comments (see also Dunlop & Fetzer 1993, p. 4; Gerard 1951 p. 13; Haugeland 1981):
Let us call arrays of symbols, or texts, digital patterns. This term emphasizes the cellular or granular nature of the patterns. Digital patterns are arrays of cells or locations that contain one or another symbol. What makes them "digital" is the individuality and discontinuity of the separate bits. Digital patterns may be contrasted with analog patterns, such as line drawings and facial expressions, in which the information comprising the pattern is continuous, not discontinuously individuated into cellular bits.
Suber is by no means alone in his use of these terms as almost synonymous. Proof that the brain is continuous would assure many that digital descriptions would be inadequate. A resounding success of discrete models of the brain would likewise convince most researchers that the brain is not usefully considered analog. In this paper I will assume this synonymy and consider things which are analog to be continuous and things which are digital to be discrete[2].
2. The Debate
2.1 Arguments for Continuity
Many theoretical arguments for continuity are based on the conviction that analog machines have a richer repertoire of behaviors than their digital counterparts. For example, Churchland (1995) claims that because digital machines have access only to rational numbers, as opposed to all reals, they suffer “a potentially severe limitation on the[ir] abilities” (p. 243). Penrose (1989) has speculated that such limitations amount to an inaccessibility to consciousness. He claims that animals, like ourselves, perform noncomputable functions. However, digital machines can only perform computable functions by definition. Thus, they can not perform all of the functions that animals can. In particular then, digital machines will never be conscious. Perhaps less colorfully, Cleland (1993) argues the related point that computational devices limited to discrete numbers (i.e. Turing machines) can not compute many physically realized functions. Presumably this limitation is avoided by analog computers and brains.
Further arguments for cognitive continuity arise from a different sort of computational consideration. Consider a simple soap bubble, whose behavior can be used to compute extremely complex force-resolving functions (see Uhr, 1994). The interactions of molecular forces which can be used to represent certain macro-phenomena are far too complex for a digital computer to compute on a reasonable time scale. It is simply a fact that, in certain circumstances, analog computation is more efficient than digital computation. Coupled with arguments for the efficiency of many evolved systems, we should conclude that it is reasonable to expect the brain to be analog.
In a more practical vein, recent technologies have incorporated the strengths of analog computers into cognitively relevant systems. In particular, analog Very Large Scale Integration (aVLSI) semiconductors have been used to construct artificial cochlea and retinas with some success (Mead 1989 as in Churchland and Sejnowski 1992; Douglas and Mahowald, 1995). Such analog computers have 10 to 100 times greater computational density (i.e. computational power per unit area) and use significantly less power than their digital counterparts (Hammerstrom, 1995). Proponents of the continuity view will claim that these successes are proof of the superiority of applying analog computional methods to understanding cognitive systems.
A distinct line of argument lies in the psychological evidence for how we actually process information. Many image researchers believe that mental images are analog representations (Jeannerod 1994). If true, some argue, this implies that the information in such representations “are related in a nonarbitrary and continuous fashion to their perceptual-motor counterparts” (Paivio 1986, p. 177 as in Jeannerod 1994). Similarly, those interested in generative mimesis (e.g. mimicking of facial features by newborns) claim that human actions seem “far too metaphorical and analog in principle to fit easily into [a] kind of quasi-symbolic computational framework” (Donald 1993, p. 740). Such results suggest we more naturally traffic in analog than digital representations making it likely that the brain is analog.
2.2 Problems with Continuity
Many of the arguments rehearsed above employ questionable assumptions. Psychological arguments for analogicity assume applicability to neurophysiological descriptions of the brain. Perhaps such conclusions are simply the result of a coarse grained analysis of fundamentally digital processes. As well, the examples of analog computation proffered are extremely specialized, yet the brain seems general purpose and able to compute many functions.
However, analog computation has a far more serious concern in regards to explaining cognitive function. If computation in the brain is fundamentally analog, serious problems arise as to how parts of the brain are able to communicate (Hammerstrom, 1995). It is notoriously difficult to ‘read off’ the results of an analog computation. Analog signals, because of their infinite information content, are extremely difficult to transmit in their entirety. Particularly since brain areas seem somewhat specialized in their computational tasks, there must be a means of sending understandable messages to other parts of the brain. Not only are analog signals difficult to transmit, analog computers have undeniably lower and more variable accuracy than digital computers. This is inconsistent with the empirical evidence for the reproducibility of neuronal responses (Mainen and Sejnowski, 1995).
2.3 Arguments for Discreteness
The Physical Symbol Systems hypothesis of Newell and Simon (1976) is perhaps the most influential statement of the ‘brain as digital computer’ analogy. Around the time of its articulation, classical approaches to artificial intelligence were impressively successful, as demonstrated by programs such as Newell’s SOAR, Anderson’s ACT*, and Winograd’s SHRDLU (Gardner, 1985). This was seen as an existence proof for the discreteness of the brain: if we can use discrete machines to behave like the brain, the brain is probably discrete.
There are a number of further advantages to the symbol systems hypothesis. For one, there are precise mathematical characterizations of the limitations of this hypothesis provided by Turing’s (1950) insightful analysis. A consequence of this analysis is that implementational details become far less important since any discrete machine is formally equivalent to any other. This has provided researchers with a large repertoire of general tools for programming such machines and analyzing the results. Pragmatically, digital computers are an excellent medium for simulating human cognition.
Furthermore, the behavior of such simulations is very predictable because of the high levels of certainty built into the state transitions of digital machinery. Thus, unlike their analog counterparts, it is possible to have very general purpose machines and standards of communication between them. This allows for a functional decomposition of cognitive systems and, more importantly, provides a means of ensuring that the functional components will be able to communicate when they are reassembled.
Unrelatedly, there is a strong argument for discreteness from neurological data – the ‘look and see’ argument. We can observe neurons and notice that their behavior is typically all-or-none. Either the synaptic input currents surpass some threshold at the soma causing a spike, or they do not. As well, we can observe that the spikes tend to have a stereotypical shape. Any slight deviation from that shape does not seem to have any effect on the vesicle release when the spike arrives at the end of the axon. This has made it seem obvious to some that neurons are chunking their input into discrete packages (Cummins 1980).
2.4 Problems with Discreteness
Most of the problems with the discreteness view are implicit in the arguments for the continuity view. Briefly, discrete machines can not compute functions over real numbers, they tend to be computationally less dense than analog computers, they use more power, and they compute complex functions slowly.
However, there are other difficulties. For example, claims to an existence proof for discreteness were premature. The once successful classical artificial intelligence approach has met some theoretical barriers. Classical models are notoriously poor at describing perceptual and motor behavior (van Gelder and Port 1995). In fact, they have been unable to crack the problem of language which had seemed one of the cognitive behaviors best suited to a symbolic understanding. In general, the psychological realism of these sorts of models has been disappointing.
As well, the neurophysiological evidence for discreteness is not conclusive. Though it strongly suggests that we are discrete in state (with respect to neurons), this does not mean we are discrete in time (van Gelder 1995). Even though the spikes themselves are all-or-none, the precise distance between any two spikes can only be expressed as a real number. If these distances are the basis of neural information processing, the brain is clearly continuous.
3. The Solution
Many who have discussed the continuity debate have arrived at an ecumenical conclusion similar in spirit to the following (Uhr 1994, p. 349):
The brain clearly uses mixtures of analog and digital processes. The flow and fusion of neurotransmitter molecules and of photons into receptors is quantal (digital); depolarization and hyperpolarization of neuron membranes is analog; transmission of pulses is digital; and global interactions mediated by neurotransmitters and slow waves appear to be both analog and digital
While strictly true, the heart of the debate lies in the question of whether cognition can be explained by analog or digital processes. The strict analogicity of the depolarization of neuron membranes may be uninteresting if its analog nature does not affect the cognitive behavior of the system. Similarly, even though the transmission of neural spikes is digital, if this digitalness is not relevant to cognition (perhaps only the time between spikes is relevant) then we should not consider the brain to be digital.
Uhr’s remarks demonstrate another general characteristic of this debate: a confusion of levels. It is not at all clear that slow waves are analog as Uhr suggests. Perhaps they only seem analog because the resolution of the instrument being used to measure slow waves is inadequate to detect the digital nature of the process which underlies them. Similarly the physical symbol systems hypothesis suggests discreteness holds at the level of psychology whereas claims to continuity often lie at the physiological level of neural processing. Researchers arguing for continuity or discreteness from such disparate positions are bound to be talking past each other. In order to resolve the debate we first need an understanding of what discreteness and continuity are which will prevent such problems.
In the next four sections I provide a definition of continuity and discreteness and argue for a solution – in particular discreteness – by employing the tools of information theory. It is by realizing that the brain is a real system, subject to physical limitations and, in particular, the effects of noise which helps resolve the question of whether the brain is analog or digital.
3.1 Relative Continuity
Consider, van Gelder and Port’s (1995) claim that we can note the position of our arm at any instance in time and, by analogy or extrapolation, conclude that the same is true of all cognitive behavior. Consider also Cummins’ (1980) assertion that the behavior of a neuron is essentially discrete. Because the neuron is the fundamental unit of cognitive behavior, Cummins concludes that the brain is essentially discrete. It must strike us as odd that two such prima facie convincing arguments have opposite conclusions. This paradox was noted by Stroud (1951) during the cyberneticist debate: “I know of no machine which is not both analogical and digital” (p. 28). Perhaps a resolution to this tension has also been voiced during the debate. Pitts states the point nicely (p. 34):
Actually, the notion of digital or analogical has to do with any variable in any physical system in relation to the rest of them, that is, whether or not it may be regarded for practical purposes as a discrete variable.
Even in the brief summary of the continuous/discrete debate provided above it is plain that participants are concerned with different levels.
It is hardly surprising that there is no absolute answer to the question of whether the brain is analog or digital. Like any physical system the brain allows various levels of analysis and description. At the quantum level certain properties will be discrete (e.g. charge). At the neuronal level, those same properties are treated as continuous.
To address the relative nature of continuity, and recalling van Gelder’s (in press) distinction between discreteness in state and discreteness in time, I offer the following two definitions:
Let x be a variable along some dimension, t be time, C be a constant, Z be the integers and R be the reals:
1.
A system is discrete in time relative to a time step Dt if it is possible to choose a to such that ![]() where ti
= to + nDt
for nÎZ and CÎR.
where ti
= to + nDt
for nÎZ and CÎR.
2. A system is discrete in state along dimension x relative to a state step Dx if f(t) Î X, where X is a subset of {nDx} for nÎZ.
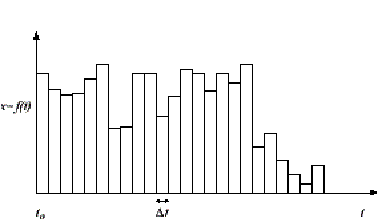
Figure 1: A system
discrete in time but not in state.
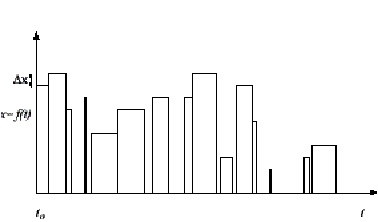
Figure 2: A system
discrete in state but not in time.
These definitions are depicted in figures 1 and 2. Expressed verbally, the first definition means that if there is a time step, for instance one second, such that at the beginning, during and at the end of all one second intervals the state of the system has remained constant then the system is discrete in time relative to one second. In order to align our measurements with the system, the definition also allows that we may choose the starting point, to, from which those one second intervals are counted off. The second definition is similar. It states that if we sample the state at any point in time and that state is always an integer multiple of some state step Dx then the system is discrete in state along that dimension[3].
Notably, both these definitions are theoretical in nature and have to be relaxed in an implementational setting. In any real system, a state change will take a certain amount of time and such transients may be variable. Because real systems take time to change states, there will always be some point (perhaps infinitesimal) in time at which the system can be in any state. As well, being in a state will seldom mean having an exact real value of x. Rather, it will mean being in some small neighborhood around x.
To account for these difficulties, we can introduce ‘slack’ parameters. Specifically, assume there is a dit such that dit << Dt and dix << Dx for all state changes i. Incorporating this parameter into the definitions, we have:
1.
A system is discrete in time relative to a time step Dt if it is possible to choose a to such that ![]() where ti
= to + nDt
for nÎZ and CÎR.
where ti
= to + nDt
for nÎZ and CÎR.
2.
A system is discrete in state along dimension x relative to a state step Dx if ![]() only at values of t where f(t)Î X, where X is a subset of {nDx +dix} for nÎZ.
only at values of t where f(t)Î X, where X is a subset of {nDx +dix} for nÎZ.
This ‘slack’ introduced into the definitions allows a small, presumably functionally insignificant, amount of time for state changes or variation in state position. In both cases, the slack terms define a margin of error which should be small compared to the state or time steps. Thus, discreteness in time becomes a discreteness with respect to a time step plus or minus a little bit. Discreteness in state can now be understood as depending on the slope of the function describing state changes. If the slope is horizontal (i.e. equal to zero) only at some values then that will be a discrete state relative to the smallest distance between those values, the state step[4].
I believe that these definitions now capture a standard notion of discreteness. Consider, for example, Von Neumann’s characterization of discreteness (1951, p. 20):
The decisive property of a switching organ [discrete component] is that it is almost always found in one or the other of its two extreme discrete states, and spends only very little time transiently in the intermediate states that form the connecting continuum.
Many definitions of the analog/digital distinction have be offered by philosophers over the years which purport to capture a similar notion (Goodman 1968; Lewis 1971; Haugeland 1981; Demopoulos 1987). However the definitions offered here are centrally implementational. This means that they do not rely on soley theoretical criteria which may be difficult to adjudicate in a real physical system (Goodman 1968; Lewis 1971; Demopoulos 1987). Though Haugeland (1981) does not fall prey to this concern, his definition does not distinguish discreteness in state from discreteness in time making it less applicable to cognitive systems as construed by cognitive science.
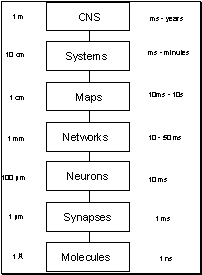
For my later evaluation of cognitive theories it is important to note that choosing a time step corresponds to choosing a level of analysis. Churchland and Sejnowski (1992) provide a figure describing the levels of analysis of human cognition. It is presented in figure 3 with the addition of approximate time scales at which the levels operate and alongside Newell’s (1990) diagram of the relation between time and human action. The resulting figure captures the approximate correlation between the time scales and levels of analysis. Figure 3 motivates the question: Given the vast range of time scales open to us, is there any principled way to decide if there is a particular level of analysis (i.e. choice of Dt and Dx) at which the brain is discrete? To answer this question we first need to determine if there are any analytic tools deemed valid by almost all cognitive scientists. If such tools exist, as I argue they do, they will provide a principled way of determining a level of analysis and we will have found a way to resolve the debate.
|
|
Scale (sec) |
Time Units |
System |
World or Theory |
|
107 |
months |
|
Social
Band |
|
|
106 |
weeks |
|
||
|
105 |
days |
|
||
|
104 |
hours |
Task |
Rational
Band |
|
|
103 |
10 min |
Task |
||
|
102 |
minutes |
Task |
||
|
101 |
10 sec |
Unit task |
Cognitive
Band |
|
|
100 |
1 sec |
Operations |
||
|
10-1 |
100 ms |
Deliberate act |
||
|
10-2 |
10 ms |
Neural circuit |
Biological
Band |
|
|
10-3 |
1 ms |
Neuron |
||
|
10-4 |
100 ms |
Organelle |
Figure 3: Levels as related to time scale. Adapted from
Churchland and Sejnowski (1992) and Newell (1990).
3.2 Information Processing
Our best scientific theories tell us that any animal in any environment must rely on its nervous system to gain knowledge of its environment. This was true for Quine (1960), and it is still true today. We know that signals are transduced from the environment by our nervous system and converted into neural spike trains. These spike trains, then, transmit information about the environment.
Even in the often diverse realm of cognitive theories, almost all researchers can agree on these points (Kitcher, 1984). Whether they hold the tenets of classical cognitive science (i.e. computationalism, symbolicism, GOFAI, etc.), or localist or distributed connectionist theory, or they prefer the dynamical systems approach or the ‘embedded’ approach they agree on these facts. Though some cognitive scientists deem themselves nonrepresentationalist (van Gelder 1995; Thelen and Smith 1994), noncomputationalist (Globus 1992), nonsymbolicist (Churchland 1989), nonconnectionist (Fodor & Pylyshyn 1988; van Gelder 1995) or nondynamicist (Eliasmith 1996) almost no one deems themselves noninformationalist[5]. Despite the often controversial uses of information theory (Clark 1993), all agree that the nervous system traffics in information. The price for denying this is just too high for most to seriously consider. Shannon (1948/1949) has provided us with powerful tools and a general framework for understanding information processing. What some have denied is not that information processing is taking place in the brain, but rather that this particular set of tools is useful for understanding the type of information processing taking place in the brain.
Their uncertainty is understandable. Any animal is in a complex, continuously varying environment. The stimulus of interest (or survival value, etc.) will likely have complex structure along many dimensions. We can characterize this problem as one of determining the continuous sensory signal given the set of spike arrival times produced by a neuron exposed to that signal. Shannon’s theory is extremely useful for quantifying the amount of information in a signal, but only when the signal has discrete states. In trying to determine the information of continuous signals we must let the sample size approach zero and the entropy then becomes infinite. In this sense, information content is not well defined for continuous variables (Reike et al. 1997, p. 109). This has lead some to conclude that we cannot usefully apply Shannon’s theory to a continuous system like the brain.
However, this conclusion is only true if we can not determine a principled discrete sample size which fully captures the behavior of a spiking neuron. If we can not determine such a sample size, we must conclude that the precise timing of spike arrivals is important to the information processing characteristics of the brain. If the precise timing is important, then an infinite amount of information is transmitted with each spike, as will be shown shortly. Put another way, if exact arrival times of spikes is important then we need a real number to express those arrival times. Real numbers can only be expressed by an infinite bit string, so each spike carries with it an infinite amount of information. In this case it is clear the that brain is continuous in its fine details (that is, relative to sub-microsecond time steps). However, if exact arrival times are not important then there is reason to think that the brain is not continuous, but rather discrete (relative to millisecond time steps).
Let me clarify and strengthen these arguments by providing more detail. As an example of the application of information theory to neural spike trains, consider the methods of MacKay and McCulloch’s (1952) paper. Probably the first application of Shannon’s theory to understanding the brain, this paper set the tone for all future analyses. Given the limitations of Shannon’s method to discrete signals, MacKay and McCulloch considered the spike train with a limited resolution. Thus they discretized the spike train into bins of width Dt and considered the presence of a spike in a bin to transmit a 1 and an absence of a spike to transmit a 0. This provides a binary representation of the spike train on which we can perform a Shannon-style analysis.
Extending this analysis, Rieke,
et al. (1997) derive the following equation to calculate the maximum entropy
rate given a presumed average firing rate, ![]() , and bin size, Dt (p. 116):
, and bin size, Dt (p. 116):
![]()
With this equation, we can determine the maximum amount of available information per spike as a function of our chosen bin size as shown in Figure 4. In this figure a spiking rate of 10Hz was used as it is the average spiking rate of pyramidal cells in the cerebral cortex. Notably, lower spiking rates increase the information transmission rate at a given bin size. However, there are both upper and lower bounds on spiking rates, making the remainder of the analysis unaffected by the particular choice of 10Hz.

Figure 4: Number
of bits of available information transmission per spike assuming a firing rate
of 10 spikes/s over a range of 10 microseconds (14.7 bits/second) to 5
milliseconds (5.5 bits/second).
These results, like those of MacKay and McCulloch determine an upper bound on information transmission rates. This means that any particular choice of coding scheme could not possibly carry more information about the input signal waveform. Rieke, et al. (1995) have shown that information transmission in the frog auditory system gets as high as 90% of this theoretical limit when presented with naturally occurring stimuli. These experiments show both that the biological systems are functioning near the physical limits of information transmission and that the coding scheme used is, as expected, most efficient for natural stimuli.
However, from the graph it is clear that as the bin size decreases, the information transmission rate increases asymptotically. Thus, if we choose a small enough bin size, we can have infinite information transmission rates and the brain’s information processing capacity is dependent on the infinitesimal precision of spike arrival times and hence continuous. How can researchers confidently make claims about the efficiency of spike train encoding in real systems if this is the case? The answer is simple. This is not the case and the reason is noise.
3.3 Noise
If there is any expectation of noise or uncertainty in the signal being passed from one neuron to the next, the precision of a neural code will drop dramatically. This is because the precise spike arrival times will no longer be used to encode the stimulus signal. Consider sending a message down a telephone wire using spike train encoding. If the wire itself introduces a small amount of noise into the signal, the distance between spikes at their destination will be slightly different from the distance between spikes as they were sent. Therefore it would be unwise and, in fact, impossible to rely on the exact distance between spikes to transmit our message. The axon, it seems, is just like our noisy telephone wire. Lass and Abeles (1975) have found that mylenated axons introduce a few microseconds of jitter over a length of about 10cm.
A few microseconds of jitter is not much noise, but there are other sources of noise as well. In particular, synapses have been found to be rather unreliable in their release of vesicles into the synaptic cleft given the presence of an action potential in the presynaptic axon (Stevens and Wang 1994). Furthermore, the amount of neurotransmitter in each vesicle can vary, as can the ability of the presynaptic neuron to release the vesicles (Henneman and Mendell 1981). Despite these various sources of noise, neurons have been shown to reproduce and respond similarly (though not identically) to similar signals (Baer and Koch 1994; Gallant, Conner et al. 1994).
Given the empirical fact of the matter concerning the noisiness of neurons and their ability to extract and pass the signal of interest, it seems the code used by neurons is a robust one, as we would hope. However, the only way it can be robust is if it does not depend on precise spike arrival times; that is, if it is discrete at some level. Reike, et al. (1997) have empirically demonstrated that coding efficiency in neurons peaks at .4 ms and actually decreases for smaller bin sizes. Thus, the various sources of noise introduce uncertainty into spike arrival times to the point where measuring the arrival times to a precision of about a half a millisecond will gain you the best reproduction of the original signal. Reike, et al. also note that this coding efficiency is within a factor of two of the physical limits set by the statistics of the spike train. Thus, no coding scheme could use such spike trains to encode more than about twice as much information regarding the stimulus signal. The information transfer rates with a time step of .4 milliseconds are about 3 bits per second. Three bits of information is far more information per spike than some have claimed (e.g. Cummins 1980, p. 189) but it is far less than the infinite amount of information needed to encode a real number. Clearly, the effects of noise on information transfer are significant. In fact, the effects are significant enough to allow us to convincingly claim that the brain is discrete in time at a time step on the order of 1 millisecond.
Researchers tend to agree that discreteness in time is more contentious than discreteness in state in the case of the brain. The ‘look and see’ argument is quite compelling for discreteness in state. Neurons do seem to be discrete in state and there are finitely many of them. Furthermore, neurons are necessary for our cognitive behavior. From these premises it is natural to conclude that the brain is discrete in state at this level of description amenable to explaining cognitive phenomena. Furthermore, we can realize that the sources of noise which limit the precision of the temporal code will also serve to limit any voltage coding on the part of the neurons (though it is not clear there is any). So even if we are currently overlooking important state differences, they will be subject to a discrete description as well.
Together, the ‘look and see’ argument for discreteness in state and the information theoretic argument for discreteness in time support the strong claim that the brain is discrete in time and state at a time step on the order of 1 millisecond and with respect to neural firings at a state step of about 70mV.
3.4 Discussion
It seems we now have an answer to the question posed by the cyberneticists some 50 years ago. They asked “whether information be continuously coded or discretely coded” (McCulloch 1951, p. 43). We can confidently answer: “Discretely.” How have we arrived at this answer? Recall that first we needed relative definitions of discreteness in time and state. By examining an information theoretic analysis of the neural spike train, we saw how it is possible to establish an upper bound on possible information transmission at a given temporal resolution. In the case of real systems, any expectation of noise will make the temporal resolution drop dramatically. Current neurophysiological evidence suggests that the temporal resolution necessary or adequate for understanding the neural code is on the order of one millisecond. At this resolution, neurons seem to transmit between about 3 and 7 bits of information per spike or about 300 bits per second (Rieke 1997). This means, of course, that another implementation able to transmit information at a similar rate should be able to have the same information processing characteristics as the brain[6].
The assumptions needed to arrive at this conclusion are minimal. We have to hypothesize that cognitive function, broadly construed, is information processing. We have to assume that all the information processed by the brain is coded in the neural spike train before it is cognitively relevant. This latter assumption may seem contentious, if we consider the effects of hormones or other holistic effects which may change our cognitive function. However, these sorts of effects will merely moderate the functioning of neurons. It would be unlikely if they could enable a neuron to pass more information than normal, though they may cause it to pass information differently. In any case, they will not eliminate noise and thus any effects are still bound by the above analysis.
Many will be discomforted to know that the brain can be analyzed into ‘bits’. “The brain is more like a slide rule than a digital computer,” they will protest. However, if we consider a slide rule more carefully, the assumed dichotomy is not evident. For a slide rule to provide an answer to a calculation it performs, the answer must be ‘read off’ by something, probably a human eye. If the reader can not access the results of such a calculation, the result useless. Of course, the eye which must read the slide rule has a limited resolution. In fact, the physics of diffraction places limits on what it is possible for any imaging system to read off of the slide rule. The finite number of rods and cones in our retina and any visual noise introduced by the atmosphere (or reflections or movement), serve to limit the amount of information available to us when reading the continuous slide rule. The limitations are such that we can express the amount of information available from the slide rule as a number of bits.
The case is analogous in neural systems. For a neuron to receive information from its neighbor, it must examine its neighbor’s message in the presence of noise. For a neuron to send a message to its neighbor, it must encode the message in the presence of noise. It is truly amazing at how effective neurons are at preserving the information they pass through encoding and decoding spike trains. In fact, neural systems approach the theoretical limits of coding efficiency. Nevertheless, there is a finite amount of information passed per neural spike. This allows us to consider the system as discrete in time on a time scale of about one millisecond.
4. Consequences for Cognitive Science
As long ago as 1951, it was suggested that the information passed by neurons is contained in the spike trains (Von Neumann 1951, p. 31). Now we can quantify that hypothesis. Not surprisingly, this has important consequences for the theoretical claims underlying the various research programs of cognitive science. In what follows, I will consider the significance of the preceding discussion for symbolicism (or classicism, or computationalism), connectionism, and the more recently proposed dynamicist view of cognition.
4.1 Symbolicism
It would seem that symbolicists should celebrate an analysis which concludes that the brain is fundamentally discrete, as they are typically thought to be the major proponents of such a view. However, discreteness being a relative attribute, it is significant that discreteness claims can be made at different levels. Unlike the position just presented, symbolicist claims are seldom explicit about the time step relative to which the system is supposed to be discrete. Van Gelder (1995) has argued strongly that symbolicists do not take time seriously in their models. This oversight on the part of symbolicists renders their discreteness claims difficult to evaluate or, more often, indefensible at the implicit level of analysis.
In cases where time is discussed, the systems constructed do not adhere consistently to any one level of temporal analysis. Consider, for example, Newell’s (1990) book length discussion of symbolic computation in the context of his SOAR model. On the basis of neurological data, Newell explicitly identifies a time step relative to which the system is discrete; 10 milliseconds. The system is discrete at this level because this is how long it takes to execute a production in the SOAR system. However, productions range from encoding whether or not a light is on or off (p. 275) to: “If the problem space is the base-level-space, and the state has a box with nothing on top, and the state has input that has not been examined, then make the comprehend operator acceptable, and note that the input has been examined” (p. 167). There is little reason to think these productions would both be executed in the same length of time. If the 10ms time step is to be a rigorous constraint we deserve an explanation of why productions of seemingly disparate complexity would be executed in one time step. This difficulty has arisen because the number of productions per step in the model has been chosen to approximate human performance only on certain tasks. When generalized from these tasks to others, the hypothesized time step is no longer realistic (see, for example, pp. 274-282).
Thus, even Newell’s ‘time conscious’ modeling efforts are unconvincing in their ability to provide an argument for discreteness. As well, most of the symbolicist models assume discreteness at an even higher level. Dynamicists have provided lengthy critiques of why such models are often contradicted by human behavior (Thelen and Smith 1994; Globus 1992; van Gelder 1995).
4.2 Connectionism
The results in section 3, that neurons should not be modeled as encoding real numbers, is an important constraint on connectionist models. Paul Churchland (1995) has made a point of trying to distinguish connectionist models from symbolicist ones on the basis of their continuity (p.243):
Genuinely parallel implementation is important for the further reason that only then will the values of all of the variables in the network... have open to them every point in the mathematical continuum. So-called "digital" or discrete-state computing machines are limited by their nature to representing and computing mathematical functions that range over the rational numbers...This is a potentially severe limitation on the abilities of a digital machine...Therefore, functions over real numbers cannot strictly be computed or even represented within a digital machine. They can only be approximated.
Such claims are simply misleading. Just like digital machines, neurons can only approximate functions over real numbers. However, there are many connectionists who have directly addressed the questions of the noisiness of real neurons (Mainen and Sejnowski 1995), and are well aware of the importance of time (see Churchland and Sejnowski 1992 for numerous examples).
Different approaches to connectionism should consider different aspects of this analysis. Connectionists who feel is important that their models are continuous, or who have such assumptions built into their models, should rethink their position. Connectionists who rely on static or localist models should realize that they will run into many of the same difficulties encountered by the symbolicists when trying to account for the information characteristics of the brain (see previous section). In sum, connectionists should be aware of the consequences of the various assumptions they make when constructing their models. The less likely those assumptions are to conflict with the information capacities of the brain, the more plausible the models they provide.
4.3 Dynamicism
The application of dynamical systems theory to understanding the brain has been welcomed, and suggested, by many (Skarda & Freeman 1987; Churchland & Sejnowski 1992). Many of these are connectionists, and so it is not surprising that the consequences of an information theoretic analysis for connectionism are should be equally applicable to dynamicism. As for connectionists, claims such as: “the system's entire operation is smooth and continuous; there is no possibility of nonarbitrarily dividing its changes over time into distinct manipulatings, and no point in trying to do so” (van Gelder 1995, p. 354) are false on the analysis in section 3.
However, for those dynamicists who wish to be non-connectionists (e.g. van Gelder and Port, 1995; Thelen and Smith 1994), new concerns arise. In particular, the insistence of some researchers that only low-dimensional dynamical descriptions are necessary for describing cognition introduces further difficulties (van Gelder 1995; van Gelder and Port 1995). Because they assume low-dimensional models, these dynamicists must posit continuous ‘collective’ parameters which aggregate the behavior of many neurons. This poses some important problems. For one, it is not clear that there is a principled way to discover such parameters (Eliasmith 1996; 1997). As well, it is not clear with respect to what time or state step such parameters are to be considered continuous. Normally, these parameters are treated as ‘completely’ continuous (see van Gelder 1995) but the analysis here suggests this is not true of the brain. More importantly, it is not at all clear if such parameters can, in principle, preserve the information processing capacities of the brain. Assuming that low-dimensional models are capable of capturing the high-dimensional behaviors of the brain is dangerous. We can characterize the high-dimensional information processing capacities, but we do not know how continuous approximations of underlying finite processes affect overall system behavior.
5. Conclusion
In retrospect, Kant seems to have identified both the deeper source of the debate and, implicitly, its resolution. He notes that the tension between continuity and discreteness arises from a parallel tension between the certainty of theory and the uncertainty of how the real world is; in short, between theory and implementation. If we focus on theory, it is not clear that the continuity of the brain can be determined. But, since the brain is a real world system, implementational constraints apply. In particular, the effects of noise on limiting information transfer allow us to quantify the information transmission rates of real neurons. These rates are finite and discretely describable. Thus, a theory informed by implementation has solved our question, at least at one level of description.
Whether the brain is discrete at a higher level of description is still open to debate. Employing the provided definitions, it is possible to again suggest that the brain is discrete with a time step of 10ms as first proposed by Newell. Empirical evidence can then be brought to bear on this question, likely resulting in its being disproved. Similarly, one might propose that the brain is continuous at a similar level of description. Again, empricial evidence can be used to evalute such a claim. However, what has been shown here is that the brain is not continuous ‘all the way down’. There are principled reasons for considering the cognitively relevant aspects of the brain to be discrete at a time step of about one millisecond. In a sense, this does not resolve all questions concerning the analogicity of the brain, but it resolves perhaps the most fundamental one: Can the brain ever be considered digital for explaining cognitive phenomena? The answer, it seems, is “Yes”.
6. References
Blachowicz, J. (1997). “Analog representation beyond mental imagery.” The
Journal of Philosophy. 94(2): 55-84.
Churchland, P. (1989). A neurocomputational perspective. Cambridge, MA,
MIT Press.
Churchland, P. (1995). The engine of reason, the seat of the soul: a
philosophical journey into the brain. Cambridge, MA, MIT Press.
Churchland, P. S. and T. Sejnowski (1992). The computational brain.
Cambridge, MA, MIT Press.
Clark, Austen (1993). “Mice, shrews, and misrepresentation.” The Journal
of Philosophy. 90(6): 290-310.
Cleland, C. (1993). “Is the Church-Turing thesis true?” Minds and
Machines 3: 283-312.
Cummins, R. (1980). Functional analysis. Readings in philosophy of
psychology. N. Block. Cambridge, MA, Harvard University Press. 1: 185-190.
Demopoulos, W. (1987). “On some fundamental distinctions of
computationalism.” Synthese 70:
79-96.
Dennett, D. (1991). “Real patterns”. The Journal of Philosophy. 88(1): 27-51.
Donald, M. (1993). “Precis of Origins of the modern mind: Three stages in
the evolution of culture and cognition.” Behavioral & Brain Sciences 16(4): 737-791.
Douglas, R. and M. Mahowald (1995). Silicon neurons. The handbook for
brain theory and neural networks. M. Arbib (ed). Cambridge, MA, MIT Press.
Dunlop, C. and J. Fetzer (1993). Glossary of cognitive science. New York,
NY, Paragon.
Eliasmith, C. (1996). “The third contender: a critical examination of the
dynamicist theory of cognition.” Philosophical Psychology 9(4): 441-463.
Eliasmith, C. (1997). “Computation and dynamical models of mind.” Minds
and Machines 7: 531-541.
Fodor, J. (1983). The modularity of mind. Cambridge, MA, MIT Press.
Fodor, J. and Z. Pylyshyn (1988). “Connectionism and cognitive
architecture: A critical analysis.” Cognition 28: 3-71.
Gardner, H. (1985). The mind's new science. New York, Basic Books.
Gerard, R. (1951). “Some of the problems concerning digital notions in
the central nervous system.” Cybernetics: Proceedings of the 7th Macy
Conference. H von Foerster (ed.). New York, NY, Macy Foundation. pp. 11-57.
Globus, G. G. (1992). “Toward a noncomputational cognitive neuroscience.”
Journal of Cognitive Neuroscience 4(4):
299-310.
Goodman, N. (1968). Languages of art. Indianapolis, IN, Hackett
Publishing Company.
Hammerstrom, D. (1995). Digital VLSI for neural networks. The handbook of
brain theory and neural networks. M. Arbib. Cambridge, MA, MIT Press.
Haugeland, J. (1981). “Analog and analog.” Philosophical Topics 12: 213-26.
Henneman, E. and L. Mendell (1981). Functional organization of motoneuron
pool and its inputs. Handbook of physiology :The nervous system. V. B. Brooks.
Bethesda, MD, American Physiological Society. 2.
Jeannerod, M. (1994). “The representing brain: Neural correlates of motor
intention and imagery.” Behavioral & Brain Sciences 17(2): 187-245.
Kitcher, P. (1984). “In defense of intentional psychology.” The Journal
of Philosophy. 81(2): 89-106.
Lass, Y. and M. Abeles (1975). “Transmission of information by the axon.
I: Noise and memory in the myelinated nerve fiber of the frog.” Biological
Cybernetics 19: 61-67.
Lewis, D. (1971). “Analog and digital.” Nous 5: 321-7.
MacKay, D. and W. S. McCulloch (1952). “The limiting information capacity
of a neuronal link.” Bulletin of Mathematical Biophysics 14: 127-135.
Mainen, Z. F. and T. J. Sejnowski (1995). “Reliability of spike timing in
neocortical neurons.” Science 268:
1503-1506.
Maudlin, J. (1989). “Computation and consciousness.” The Journal of
Philosophy. 86(8): 407-432.
Newell, A. (1990). Unified theories of cognition. Cambridge, MA, Harvard
University Press.
Newell, A. and H. Simon (1976). “Computer science as empirical enquiry:
symbols and search.” Communications of the Association for Computing Machinery 19: 113-126.
Paivio, A. (1986). Mental representations: A dual coding approach.
Oxford, Clarendon Press.
Penrose, R. (1989). The Emperor's New Mind. Hillsdale, NJ, Erlbaum.
Quine, W. V. O. (1960). Word and object. Cambridge, MA, MIT Press.
Rieke, F., D. Bodnar and W. Bialek (1995). Naturalistic stimuli increase
the reate and efficiency of information trnasmission by primary auditory
neurons, Proceedings of the Royal Society of London. Series B, 262, 259-265.
Rieke, F., D. Warland, et al. (1997). Spikes: Exploring the neural code.
Cambridge, MA, MIT Press.
Searle, J. R. (1990). “Is the brain a digital computer?” Proceedings and
Addresses of the American Philosophical Association 64: 21-37.
Shannon, C. (1948/1949). A mathematical theory of communication. In: The
mathematical theory of communication. C. Shannon and W. Weaver. Urbana, IL,
University of Illinois Press: 623-656.
Skarda, C. A. and W. J. Freeman (1987). “How brains make chaos in order to
make sense of the world.” Behavioral and Brain Sciences 10: 161-195.
Smolensky, P. (1988). “On the proper treatment of connectionism.”
Behavioral and Brain Sciences 11(1):
1-23.
Stevens, C. F. and Y. Wang (1994). “Changes in reliability of synaptic
function as a mechanism for plasticity.” Nature 371: 704-707.
Suber, P. (1988). “What is software?” Journal of Speculative Philosophy 2(2): 89-119.
Thelen, E. and L. B. Smith (1994). A dynamic systems approach to the
development of cognition and action. Cambridge, MIT Press.
Turing, A. M. (1950). “Computing machinery and intelligence.” Mind 59: 433-460.
Uhr, L. (1994). Digital and analog microcircuit and sub-net structures
for connectionist networks. Artificial intelligence and neural networks: Steps
toward principled integration. V. Honavar and L. Uhr. Boston, MA, Academic
Press: 341-370.
van Gelder, T. (in press). “The dynamical hypothesis in cognitive
science.” Behavioral and Brain Sciences.
van Gelder, T. (1995). “What might cognition be, if not computation?” The
Journal of Philosophy XCI(7):
345-381.
van Gelder, T. and R. Port (1995). It's about time: An overview of the dynamical approach to cognition. Mind as motion: Explorations in the dynamics of cognition. R. Port and T. van Gelder. Cambridge, MA, MIT Press.