Eliasmith, C. & P. Thagard.
(2001) Integrating Structure and Meaning: A Distributed Model of Analogical
Mapping. Cognitive Science.
(Chris Eliasmith,
Philosophy-Neuroscience-Psychology Program, Department of Philosophy,
Washington University in St. Louis, Campus Box 1073, One Brookings Drive, St.
Louis, MO 63130-4899, chris@twinearth.wustl.edu)
(Paul Thagard, Department of Philosophy,
University of Waterloo, pthagard@watarts.uwaterloo.ca).
Integrating Structure and Meaning: A Distributed Model of Analogical Mapping*
Abstract
In this paper we present Drama, a distributed model of analogical mapping that integrates semantic and structural constraints on constructing analogies. Specifically, Drama uses holographic reduced representations (Plate 1994), a distributed representation scheme, to model the effects of structure and meaning on human performance of analogical mapping. Drama is compared to three symbolic models of analogy (SME, Copycat, and ACME) and one partially distributed model (LISA). We describe Drama’s performance on a number of example analogies and assess the model in terms of neurological and psychological plausibility. We argue that Drama’s successes are due largely to integrating structural and semantic constraints throughout the mapping process. We also claim that Drama is an existence proof of using distributed representations to model high-level cognitive phenomena.
1. Introduction
Most connectionist models focus on low-level cognitive tasks such as categorization, recognition, and simple learning (Churchland and Sejnowski, 1992). Critics of connectionism often contend that these models, though impressive in some ways, have little to do with high-level human cognition (Fodor and Pylyshyn, 1988; Fodor and McLaughlin, 1990; c.f. Bechtel, 1995).
Analogy-making (or analogizing) is a quintessential high-level cognitive function that is only fully developed in humans (Holyoak and Thagard, 1995). The process of mapping relations and objects that describe one situation (a source) to another (a target) in a systematic way involves an understanding of the semantics and structure of both the source and target. Until recently, connectionist distributed representations have provided no effective means of capturing the complex embedded structure needed to perform such tasks (Plate, 1994). Although there is general agreement among connectionists and neuroscientists that representation in the brain is distributed, distributed computational models of tasks as structure dependent as analogy have not been forthcoming (Hinton, 1986; Miikkulainen and Dyer, 1988; Smolensky, 1988; Churchland, 1989; Churchland and Sejnowski, 1992). However, distributed representations do seem to provide powerful accounts of the semantics of cognition (Gentner and Forbus, 1991; Churchland and Sejnowski, 1992; Harnad, 1992; Plate, 1994).
In contrast, symbolic representations, which are ideally suited to providing flexible representations of structure, are often criticized as being semantically brittle (Hinton, 1986; Clark and Toribio, 1994). Nevertheless, most current models of human analogy-making rely on symbolic representations at the expense of providing inadequate accounts of the effects of semantics on the analogical mapping process (Mitchell, 1993; Hofstadter, 1995).
Clearly then, a model of analogy that employs a means of representation that is both structurally and semantically sensitive would be an improvement over current models. Furthermore, it has been argued that high-level cognitive processing, in particular linguistic processing, is best explained by the integration of structure and meaning (Tomasello, 1998; Langacker, 1986). There are two possible ways of achieving this goal:
1. Improve the semantic flexibility of symbolic representations (see Barnden, 1994 for further discussion).
2. Improve the structural flexibility of distributed representations.
We have chosen the second option for a number of reasons (see section 3 for details). In particular, distributed representations: can be learned from the environment of the cognizer (Hinton, 1986); are equally applicable to all modes of perception (i.e. vision, hearing, olfaction, etc.); have recently been extended to provide an effective means of capturing embedded structure (Smolensky, 1990; Plate, 1993); and provide a degree of neurological realism not found in symbolic models (Churchland and Sejnowski, 1992; Churchland, 1995). In addition, providing a distributed model of the analogical mapping process would validate the contentious claim that connectionist methods will scale to the complexity of high-level human cognition.
In the remainder of this paper, we present a computational model of analogy-making called Drama (Distributed Representation Analogy MApper). Drama combines recent advances in distributed representation of structure and an established theory of analogy to account for current psychological data on analogy-making in humans. Drama is based on Holyoak and Thagard’s (1989a) previous model of analogy, ACME, but significantly extends and improves both the number of mapping phenomena accounted for and the degree of neurological and psychological plausibility. As well, Drama, unlike ACME, embodies a theoretical commitment to explaining cognitive function through the integration of structure and semantics. Furthermore, Drama, while being a model of a high-level cognitive phenomena, is based on distributed representations – this is a feat some have though would not be possible (Gentner and Markman, 1993; section 6.2).
We begin our discussion of Drama by recounting the multiconstraint theory of analogy. We then review three other computational models of analogy (ACME, SME and Copycat), which serve as points of comparison to Drama. Subsequently we discuss holographic reduced representations (HRRs), which are the form of distributed representation used to provide structural and semantic sensitivity to Drama. After briefly outlining Drama’s architecture and algorithms, we describe Drama's performance on several real-world analogies. Next, we provide an evaluation of Drama by contrasting it with ACME, SME, and Copycat. Finally, we discuss Drama in relation to another model of analogical mapping, LISA, which has also been put forward as a distributed model of analogy (Hummel and Holyoak, 1997). We find that, though Drama has some important limitations, its current performance and its potential for improvement surpass that of other models.
2. Theories of Analogy
Current theories of analogizing tend to divide the process into three or four stages. For our purposes, analogy-making can be divided into three distinct steps (Falkenhainer, Forbus et al., 1989; Eskridge, 1994; Holyoak and Thagard, 1995). Assuming that the agent already has access to a description of the target of the analogy, the first step is to retrieve an appropriate analogous situation (i.e., the source). Next, the correspondences between propositions, objects, and relations (referred to collectively as elements of the analogy) must be found and mapped onto one another. Finally, the newly formed analogy is applied in some manner, whether it be to induce an outcome, to describe or explain a novel situation, or to generate a new schema for understanding the world. In sum, the process of analogizing consists of: retrieval; mapping; and application.
Drama is centrally concerned with the mapping stage of the analogy-making process. However, the representational commitments of Drama have been used to construct a single step model of the retrieval stage as well (Plate, 1994; Plate forthcoming). Combined, these two models account for the first two phases of analogizing (see section 6 for further discussion of Plate’s (forthcoming) model and a simple extension to Drama).
The mapping stage of analogizing is commonly the focus of computational models of analogy. The three computational theories of analogy-making instantiated by Copycat (Hofstadter and Mitchell, 1988), SME (Structure Mapping Engine) (Falkenhainer, Forbus et al., 1989), and ACME (Holyoak and Thagard, 1989) provide a cross-section of available theories of analogical mapping. Although there are many other models of analogy-making (Kedar-Cabelli, 1988; Hall, 1989), these three models are arguably the best-known and have previously been the subjects of critical comparisons (Mitchell, 1993). There is a fourth analogical theory that is of particular interest because it, too, is touted as a distributed model of analogical processing. This fourth theory, implemented in the model LISA (Hummel and Holyoak, 1997), will be discussed separately because there are a number of distinct issues that are of importance in comparing this model with Drama (see section 7).
As competitors, there are a number of issues on which the three theories diverge. However, as theories of analogizing, there are also striking similarities. The multiconstraint theory of analogy which underlies ACME (Holyoak and Thagard, 1995) captures these similarities, and is thus promising as a general theory. Notably, adherents of both Copycat and SME have provided arguments affirming the importance of each of the constraints in the multiconstraint theory (Gentner and Toupin, 1986; Falkenhainer, Forbus et al., 1989; Mitchell, 1993). Thus, there is a measure of agreement on the importance of the central tenets of the multiconstraint theory to analogy-making (Kedar-Cabelli, 1988; Hall, 1989), making it a good theory to adopt. In addition, the theory is simple, identifying only three constraints. As well, the theory is easily distinguished from its implementation in the model ACME. This allows us to separate theory from model, providing a means to reconsider the model without having to completely reinvent the theory.
The multiconstraint theory identifies three soft constraints on a good analogy: structure, similarity, and purpose. These constraints are considered “soft” because none of them must be satisfied, though each guides the construction of any analogy. Briefly, the constraint of structure guides the analogy towards one-to-one and structurally consistent mappings (see section 2.1). Similarity refers to conceptual similarity in verbal analogies (like those addressed in Drama) but also extends to visual similarity, auditory similarity, etc. for non-verbal analogies (Shelley, 1996; section 2.2). The constraint of purpose guides the analogy towards the accomplishment of practical goals as defined by the analogizing agent. In the following three sections we examine each constraint in turn and discuss their relation to ACME, SME, Copycat and Drama.
2.1. Structure
An analogy satisfies the structural constraint if it is a one-to-one mapping and structurally consistent (Gentner, 1983). A mapping is one-to-one if each element in the source corresponds to one element in the target. A mapping is structurally consistent if the objects of mapped relations are also mapped. If an analogy has both of these properties, it is considered isomorphic. In order to satisfy this constraint, two-place relations are most likely to be mapped to other two-place relations, three-place relations to three-place relations and so on. Furthermore, as figure 1 depicts, a two-place relation in which the first place contains another (two-place) relation is more likely to be mapped to a relation with that same structure than to a two-place relation with a (two-place) relation in its second place or to one with no relations in either place. In other words, the more isomorphic propositions are, the more likely they are to map to each other. Notably, the meaning of the relations and their place holders is strictly irrelevant to the constraint of structure. Thus, arbitrary letters have been used in figure 1 to label objects and relations.
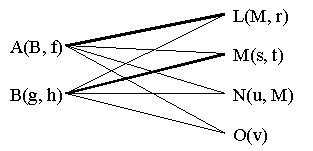
Figure 1. Two sets of relations whose degree of isomorphism is proportional to the strength of the joining lines. Arbitrary letters are used to identify objects and relations to stress that meaning is irrelevant to the constraint of structure.
Because structure has long been studied in logic and linguistics, and because structure is easy to capture in programming languages such as LISP, it is at the heart of most models of analogy. The most structurally driven model is the aptly named SME (Structure Mapping Engine) model. In this model, objects are placed in correspondence based almost entirely on their role in relational structures, with the only semantic constraint being one of identity (Falkenhainer, Forbus et al., 1989). ACME also relies heavily on the syntactic information in the source and target, though not to the same degree as SME (see section 6.2). In both cases, this reliance has been justly criticized as providing psychologically unrealistic, overly powerful and somewhat unguided mappings (Mitchell, 1993; Hofstadter, 1995; Hummel and Holyoak, 1997).
2.2. Similarity
In verbal analogies, the similarity constraint directs an analogizer to prefer semantically similar mappings. Thus, concepts with similar meaning are more likely to be mapped than those with dissimilar meaning – if there are two equally isomorphic mappings to a given element of an analogy, the more semantically similar of the two will be chosen as the best mapping. Though there is evidence that this constraint guides human analogy-making, it is often violated by humans on the basis of structural concerns (Gentner and Toupin, 1986). Violations of the constraint are more likely at the more concrete the levels of mapping. Thus, dissimilar objects are more often mapped than dissimilar first-order relations, and dissimilar first-order relations are more often mapped than dissimilar second-order relations[1].
The three models of analogy we have chosen to discuss account for semantics in very distinct ways. SME only takes into account identity semantics (i.e. ‘cause’ means the same as ‘cause’) and otherwise maps purely on the basis of structure. ACME considers semantic information only after-the-fact. Specifically, semantics guides only the acceptance of best mappings (i.e. not the choice of elements to be considered for mapping). Thus, ACME includes extremely improbable mappings in its network of potential mappings (Hofstadter, 1995). As well, ACME’s semantic relations are static, hand-coded and not decomposable. Copycat, in contrast, has semantic information encoded both directly in its "Slipnet", and by the choice of which concepts are allowed to slip into each other. However, the semantic information of the letter-string domain in which Copycat operates consists only of order information about the alphabet (i.e. ‘a’ is before ‘b’, ‘b’ is after ‘a’, etc.) and a few concepts necessary for correct operation in this domain, such as 'rightmost', 'leftmost' and 'successor'. Mitchell (1993) claims that Copycat knows much about certain concepts such as 'successor group'. However, all of this knowledge is purely implicit. The system has no representation or definition of what a 'successor group' is, but rather applies the concept as defined by the system's creator. In other words, the system could not answer queries concerning concepts. Rather it can only act consistently with an external definition of a concept under certain, controlled conditions, resulting in a semantics too impoverished for complex analogies.
The most significant theoretical innovation of the Drama model comes with its implementation of the similarity constraint. Unlike previous models, Drama actually combines this constraint with the structural constraint to generate mappings. Both structure and similarity determine the outcome of the mapping process at every stage. As has been argued by the Cognitive Linguistics movement, semantics and structure may be intimately connected (Tomasello, 1998; Ungerer and Schmid, 1996; Langacker, 1986). For example, Langacker (1987) suggests "[g]rammar (or syntax) does not constitute an autonomous formal level of representation. ... There is no meaningful distinction between grammar and lexicon" (p. 2-3). Drama adopts this insight through its novel implementation of analogical mapping, combining structural and semantic considerations (see section 4 for details). Because of this theoretical commitment, Drama can successfully account for a wide range of analogical phenomena (see section 6).
2.3. Purpose
Often, the reason for which a particular analogy is made affects how it is made (Kedar-Cabelli, 1988). This phenomenon is captured through the ‘purpose’ constraint. If the agent is aware that certain elements of an analogy are more important to the purposes of the analogy, those elements will be the focus of attention and are thus more likely to be mapped.
In SME, the goals relevant to a particular analogy are not considered until a later stage of processing (i.e. during the application phase). In Copycat, all goals are a priori assumptions, and can not be altered (Mitchell, 1993). In ACME, goals are given special consideration, affecting activations during the acceptance of the best mappings. Drama does not add anything new to these models regarding the purpose constraint.
2.4 Summary
Given these considerations, the strengths and weaknesses of each model becomes more evident. SME, like all three models, effectively deals with most structural considerations but lacks an interesting semantics and leaves pragmatic considerations to the application step. CopyCat, while unique in its ability to derive its own representations, also lacks much in terms of semantics and does not consider pragmatics except implicitly. ACME is an improvement over SME because of the inclusion of some semantic and pragmatic information in the mapping process. Unlike CopyCat, ACME is not restricted to a toy domain. However, ACME only includes semantics after structural constraints have been satisfied. As well, the semantics are not decomposable (i.e. we don’t know why dogs are similar to cats) and are static. In the case of all previous models, structure and semantics are not integrated to the degree to which they seem to be in human cognition (Langacker, 1987).
This analysis allows us to summarize the theoretical advances that are incorporated into Drama and are discussed in the remainder of the paper. Drama:
1. Lessens the dominance of structure on mapping considerations while not sacrificing psychological plausibility;
2. Considers semantics and syntax in parallel allowing both to influence all stages of the mapping process and;
3. Uses fully distributed representations that explicitly encode complex concepts that can are decomposable.
3. Holographic Reduced Representations
The high-dimensional distributed representations used in Drama are referred to as holographic reduced representations or HRRs (Plate, 1994). For the purposes of this paper, these distributed representations are 512-dimensional vectors. The representations are constructed using a form of vector multiplication called circular convolution and are thus closely related to the better-known tensor products employed by Smolensky (Smolensky, 1990). The differences between and tensor products and HRRs are discussed below. Decoding of HRR representations is performed using the approximate inverse of circular convolution, an operation called correlation (see appendix A for the algebraic details of these operations). These kinds of distributed representations have been used in a number of psychological and computational models of memory (Borsellino and Poggio, 1973; Metcalfe Eich, 1985; Murdock, 1987).
The HRR sort of distributed representation are referred to as "holographic" because the encoding and decoding operations (i.e. convolution and correlation) used to manipulate these complex distributed representations are the same as those which underlie explanations of holography (Borsellino and Poggio, 1973). The convolution of two HRRs creates a third unique HRR which encodes the information present in the two previous HRRs - a process referred to as binding. Importantly, this new HRR is not similar to either of its components, though the components may be retrieved through decoding the new HRR with a correlation operator. These operations are easiest to understand through a simple illustration.[2] Let A, B and C be HRRs. If
C = A Ä B (read: C equals A convolved with B)
then
C # A » B (read: C correlated with A approximately equals B)
and
C # B » A.
Figure 2 depicts these operations as occurring on a 3-dimensional conceptual sphere.
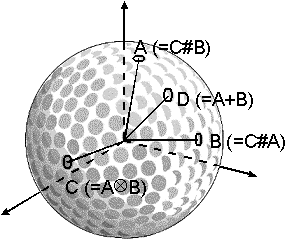
Figure 2. HRR operations depicted on a conceptual sphere. Vector C is the circular convolution of vectors A and B. Vector D is the superposition of A and B.
Another operation, superposition, is used also to combine two HRRs. Unlike convolution, superposition results in a vector equally similar to the two components. The superposition operation is simply the normalized sum of two vectors, and is written: D = A + B (see figure 2). One can think of the superposition of two vectors as being like superimposing two photographic images. The resulting image is similar in many ways to both of the original photographs, and the original images are likely to be recognized from the superimposed image, but it would be very difficult to perfectly reconstruct either of the original images. Similarly, superimposing two vectors results in a vector that is very similar to the original two vectors but cannot provide a perfect reconstruction of the original vectors. This contrasts with convolution, in which the resulting vector is nothing like the original two vectors; in fact, the expected similarity of either of the original vectors to their convolution is zero (Plate, 1994).
As with the photographic image, some of the information in the original HRR vectors is lost in their combination. Hence, HRRs are considered 'reduced' representations. Upon encoding a new representation from a number of others (e.g. constructing the representation for a particular 'cherub' from 'baby', 'has-wings', 'fictional', 'pink', etc.), the new representation does not contain all of the information present prior to encoding; the new representation is noisy. This is the case for both convolution and superposition. Therefore, when decoding a vector using the correlation operator, the resulting vector must somehow be recognized by the system, or ‘cleaned-up’.
The process of recognizing a vector is accomplished through use of the dot product. The dot product of two vectors is the sum of the product of each of the corresponding elements of the vectors. For normalized vectors, the resulting scalar is equivalent to the length of one of the vectors projected on to the other (see figure 3). This relative length value can be used as a measure of the vectors’ similarity. Because all of our conceptual vectors are normalized to the unit hypersphere, we use the dot product operation to determine the similarity of any two vectors.
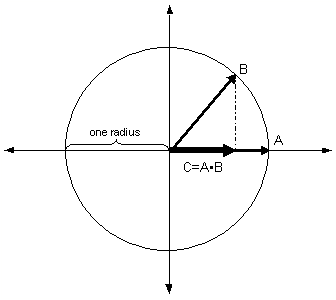
Figure 3. The dot product of normalized vectors A and B as the projection of B onto A.
A number of properties of HRRs make them promising candidates for modeling human cognition. First, HRRs are distributed representations, with all of the benefits associated with distributed representations. Thus they: are sensitive to statistical input (Smolensky, 1995); provide cross-modal representations (e.g. they have been applied to visual (Qian and Sejnowski, 1988; Raeburn, 1993), olfactory (Skarda and Freeman, 1987), auditory (Lazzaro and Mead, 1989) and tactile problems); degrade gracefully (Churchland, 1992); are semantically sensitive; represent concepts continuously; can be processed in parallel; and are subject to the many learning algorithms already developed (Hinton, 1986; Gorman and Sejnowski, 1988; Miikkulainen and Dyer, 1988; Le Cun, Boser et al., 1990; Plate, 1993). In regards to this last property (i.e. learning), it is the contents of HRRs that are the subject of these well established learning methods. The operations which encode and decode these contents (convolution and correlation) are hypothesized to be primitive operations (see Borsellino and Poggio, 1973).
Second, HRRs accommodate arbitrary variable binding through the use of convolution. Third, HRRs can effectively capture embedded structure (Plate, 1994; forthcoming). Fourth, unlike tensor products, and most other distributed representations which use vector multiplication, HRRs are fixed dimension vectors. Thus, convolving two three-dimensional vectors results in another three-dimensional vector - not a six- or nine-dimensional vector as with tensor products. Consequently, HRRs are not subject to an explosion in the size of representations as the structures represented become more complex. This property also allows HRRs of various structural depths to be easily comparable to each other without "padding" the representation, as is necessary with tensor products. Fifth and finally, convolution can be implemented by a recurrent connectionist network (Plate, 1993). This potential for implementation in recurrent networks supports the neurological plausibility of HRRs. Though the degree of neurological realism reached by such networks may be disputed, it is likely that the extent of their neurological realism is greater than that of either localist connectionist or symbolic models (Smolensky, 1995).
Most important to Drama are the properties relating to structure and semantics. The ability of HRRs to accommodate arbitrary variable bindings and embedded structure allow Drama to handle structures as complex those in classical symbolic systems. The statistical and semantic sensitivity of HRRs allow Drama to handle conceptual meaning as well as any distributed connectionist system. Thus, the representational commitment of Drama to HRRs gives it both the semantic sensitivity and the structure sensitivity needed to effectively model analogical mapping.
Table 1
Summary Comparison of the Properties of Three Forms of Representation.
|
Property |
Symbolic |
Tensor Products |
HRRs |
|
Sensitive to statistical input |
No |
Yes |
Yes |
|
Cross-modal representation |
No |
Yes |
Yes |
|
Graceful degradation |
No |
Yes |
Yes |
|
Semantically sensitive |
No |
Yes |
Yes |
|
Continuous representation of concepts |
No |
Yes |
Yes |
|
Easily processed in parallel |
No |
Yes |
Yes |
|
Neurologically plausible |
No |
Yes |
Yes |
|
Arbitrary variable binding |
Yes |
Yes |
Yes |
|
Embedded structure |
Yes |
Yes |
Yes |
|
Noise-free representation |
Yes |
Yes |
No |
|
Perfect encoding/decoding |
N/A |
Yes |
No |
|
Fixed dimension representation |
N/A |
No |
Yes |
|
Cross-level comparison |
Yes |
No |
Yes |
A summary comparison of the properties of HRRs, tensor products and symbolic representations is presented in table 1. The next section discusses Drama's application of HRRs to analogizing.
4. Drama's Algorithms
Drama is intended as a model of human analogy-making abilities. Using HRRs as the representational foundation for Drama provides a powerful means of manipulating the sets of propositions which make up a verbal analogy. However, Drama’s representational commitment does not determine the mapping process itself. We discuss the mapping algorithm used by Drama in this section.
Drama's particular implementation of the mapping process is based on the multiconstraint theory outlined in section 2. The original implementation of the theory in ACME has provided the multiconstraint theory with some empirical support (Holyoak and Thagard, 1989). As well, ACME provides a useful comparison to Drama's implementation of this theory. As with ACME, the mapping process has been subdivided into two main parts: constructing the mapping network; and settling the mapping network. However, the algorithm for constructing the mapping network is new, having been informed by the limitations of ACME. In particular, Drama combines the structural and semantic constraints which ACME implemented independently. This synthesis results in many behaviors more psychologically realistic than those of ACME (see sections 5 and 6).
The mapping network is a network whose nodes are possible mappings and whose connections are inhibitory or excitatory links connecting those nodes. This network is constructed to encapsulate the constraints of structure, similarity and purpose which guide the system to choose the best mappings among those that are likely. Settling of the network is equivalent to satisfying as many of the constraints in parallel as is possible. Justification of this choice of decomposition of the analogy-making task has been discussed at length elsewhere (Holyoak and Thagard, 1989; Thagard, Holyoak et al., 1990; Holyoak and Thagard, 1995). The procedures for constructing and settling the network in Drama are discussed below.
Before tackling the technical details of Drama, it is useful to introduce the Cupid analogy that will serve as an illustrative example in our explanations of the functioning of Drama. This (somewhat degenerate) analogy is expressed in the following sentence:
When I first saw her radiant beauty I had a pang as if my heart felt
Cupid's arrow.
An analytic presentation of the analogy can be found in table 2.
Table 2
Structure of the Cupid Analogy
|
Source (Cupid's Arrow) |
Target (Love Pang) |
|
C1: The heart feels the arrow. |
P1: The observer sees radiant beauty. |
|
C2: The observer's heart hurts. |
P2: The observer has a pang. |
|
C3: C1 causes C2 |
P3: P1 causes P2 |
Table 3 identifies the expected result of mapping this analogy. Though simple, this analogy has object, relational (first-order), and systems (second-order) mappings making it a sufficiently complex example to show the basic functioning of Drama (see section 2).
Table 3a
Mappings in the Cupid Analogy
|
Source (Cupid's Arrow) |
Target (Love Pang) |
|
arrow |
radiant beauty |
|
heart |
observer |
|
hurt |
pang |
|
feels |
sees |
|
cause |
cause |
The next three sections describe the steps necessary for Drama to solve such an analogy. These include encoding the input into HRRs, using these representations to create the mapping network, and finally settling the mapping network to determine the best mappings for this analogy.
4.1. Inputs
For Drama to represent “concepts” for a particular analogy, it must generate random, normalized, 512-dimensional vectors. This is equivalent to picking a random point on the surface of the conceptual sphere and assigning it a particular name. In a "real-world" system, such a representation could be learned through interaction of the system with its environment (see section 3). However, this process is beyond the scope of our current model.
In order to capture the structure of propositions, we bind the various elements of a proposition to their appropriate places. Thus, in order to represent proposition C1 “The heart feels the arrow” we must perform the following bindings using convolution:
relation Ä feels (1)
object Ä arrow (2)
agent Ä heart (3)
These bindings can then be superimposed to give the full sentence:
C1 = relation Ä feels + agent Ä heart + object Ä arrow (4)
Proposition C1 is thus a 512-dimensional vector composed of the relevant bindings superimposed together and normalized. On a ‘conceptual sphere’, we can think of the bindings of two vectors as creating a third, unique vector (i.e. finding a distant dimple to which to assign the binding). The subsequent superposition of these unique vectors is equivalent to locating the central dimple of the group of three bound dimples and assigning the label "C1" to that dimple (see figure 4).
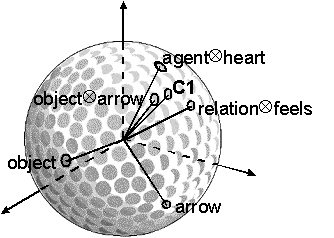
Figure 4. Superposition of three bound concepts to form proposition C1 on a conceptual sphere. The binding (i.e. convolution) of ‘object’ and ‘arrow’ is also shown.
Similar operations are used to encode properties and isa relations for the appropriate concepts used in an analogy. Properties are encoded using superimposed bindings. For example, the proposition “The observer's heart hurts” would be encoded as:
property Ä hurts (5)
C2 = heart + property Ä hurts (6)
On the other hand, isa relations are encoded using only superposition. Though there are no examples of this in the Cupid analogy, if the proposition “Cupid is fictional and a cherub” were present, it would be encoded as:
cupid = fictional + cherub (7)
To encode higher level relations, such as 'cause', one simply repeats the same process used for encoding the lower level relations. Therefore the proposition “C1 causes C2” would necessitate performing the appropriate bindings:
relation Ä cause (8)
object Ä C1 (9)
agent Ä C2 (10)
And then the superpositions:
C3 = relation Ä cause + object Ä C1 + agent Ä C2 (11)
Once the representations have been encoded as necessary, it is possible to decode them using the correlation operation. For example, if we correlate C1 with 'relation', the resulting vector is approximately equal to the 'feels' vector. Conversely, if we correlate C1 with 'feels', the resulting vector is approximately equal to the 'relation' vector. It is the cleaning up process that determines which vectors the results of correlation are nearest to (see section 3).
Given the method of encoding and decoding propositions into representations which maintain semantic and structural information, it is now possible to describe the analogy-making algorithm of Drama with reference to these representations and their operators.
4.2. Network Construction Algorithms
There are three major steps involved in creating the mapping network which Drama settles to produce the final "best" mapping. These steps are: perform the initial mapping; construct inhibitory links; and construct pragmatic links. The following subsections outlines the algorithm used to accomplish each of these steps.
4.2.1. Initial Mapping. The initial mapping step is the most important, and complicated of the three network construction steps. The algorithm constructs excitatory links between propositions of the source and target based on structural and semantic similarity in tandem. In other words, it decides which, if any, mappings are likely based on the syntax and meaning of given source and target propositions. The following eight steps present a simplified version of the original algorithm which was implemented in C++ and run on a PowerMac 7100/80 for the examples presented in section 5. All italicized words in the following description refer to variables whose typical values and definitions are given following the algorithm. The square brackets, [], denote the particular aspect of the multiconstraint theory of analogy which justifies the step (see section 2).
1. Find the dot product similarity of each source proposition vector to each target proposition vector [similarity].
2. If a particular similarity is greater than the threshold and they have the same number of constituent types,[3] create the mapping node: “Source Proposition = Target Proposition” [similarity and structure]. Seed the activation of this node with their similarity value.
3. Decode the proposition vectors into their constituents, and create the following mapping nodes if applicable: “Source Object = Target Object”, “Source Agent = Target Agent”, “Source Relation = Target Relation”, etc [structure]. Seed the activation of these nodes with their similarity value.
4. Construct excitatory links between the proposition mapping node and its constituent mapping nodes and set their value to excite [structure].
5. Construct excitatory links between each of the constituent mapping nodes and set their value to excite [structure].
6. Perform steps 3-6 for all mapped constituents (except already existent nodes) until none of the constituents can be decoded further.
7. If the “Source Object = Target Object” and “Source Agent = Source Agent” nodes are valid nodes for any other sets of two proposition vectors, map those proposition vectors as per steps 3-6 [structure].
8. If any proposition vectors in the source have not been mapped, for each of those non-mapped proposition vectors perform steps 3-7 with all target proposition vectors that have the same number of constituent types regardless of semantics [structure in case of no similarity information].
The threshold variable determines how similar elements must be to be considered similar for the purposes of mapping. The threshold is set to 0.2 in the examples we have run on Drama. If the similarity value (i.e. dot product) of A and B is above the threshold, then they are somewhat similar; otherwise, they are considered not similar. The activation variable helps to vary the likelihood of a particular node being accepted during settling: a high activation increases the chances of a node being accepted. The similarity of two items is determined by their dot product divided by the semantic similarity system parameter. This parameter determines how much weight the system puts on semantics. The excite variable determines the strength with which mutually supporting constraints aid each others' acceptance. In Drama, this variable is always set to 0.1.
If a particular node is created more than once, for each re-creation its activation seed is increased by the semantic similarity of its constituents. Similarly, if a particular excitatory link is created more than once, each time it is created the already existing link is updated by the value of an excite increase parameter. In our examples, this parameter was set to the same value as excite, which is 0.1.
Notably, these nodes currently use a localist representation in Drama. Though it is clearly possible to encode relations such as ‘maps(C1, P1)’ using HRRs, we have decided not to do so as the choice of representation type at this level should not affect analogical mapping (see appendix B for an example of a fully encoded network and discussion). Moreover, the large number of extra encoding and decoding operations demanded by a fully encoded network are too demanding for our available hardware. However, we would not expect the decoding and encoding to be slow on a parallel machine (see appendix C for a complexity analysis of the mapping process and discussion). Future versions of Drama may extend the representational scheme to all aspects of the model, but again, this should not affect the mapping process.
To clarify this algorithm, we will now trace it through some of the steps involved in mapping the Cupid analogy. First, step 1 will generate the similarity values of propositions C1 to C3 compared to P1 to P3 (i.e. C1-P1, C1-P2, C1-P3, C2-P1, etc.). Of these similarities, C3-P3 will be the greatest, as both of these propositions contain the semantically identical 'cause' concept, and structurally similar 'cause' relation (i.e. cause(agent, object)). Thus, this comparison will satisfy the 'if' condition of step 2, and step 2 will create the “C3=P3” mapping node (see figure 5).
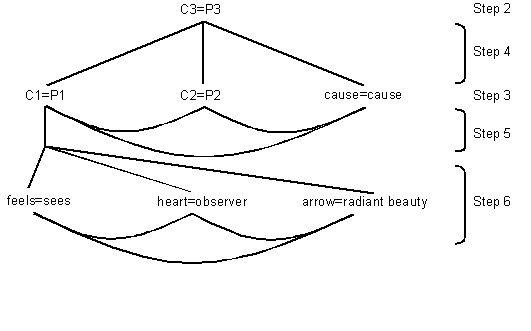
Figure 5. Example steps of the creation of the potential mapping network for the Cupid example.
Step 3 will create the nodes: “C1=P1”, “C2=P2”, and “cause=cause” and seed them appropriately
Step 4 will construct all of the excitatory links between the node “C3=P3” and the nodes “C1=P1”, “C2=P2”, and “cause=cause”.
Step 5 will construct all of the excitatory links between the nodes “C1=P1”, “C2=P2”, and “cause=cause” (see figure 5).
Step 6 causes us to select a current constituent node, let us say “C1=P1” and treat it as we have just treated the proposition node “C3=P3”. Thus, we will decode propositions C1 and P1, and map their constituents, resulting in the mappings “arrow=radiant beauty”, “heart=observer”, and “feels=sees”. The appropriate links will be constructed, as they were for the higher-level mapping “C3=P3” (see figure 5).
Since none of the constituents of “C1=P1” can be further decoded into constituents, step 6 would be bypassed at this point. However, step 6 must be performed for the constituents “C2=P2” and “cause=cause” of the proposition node “C3=P3”.
Step 7 is not necessary for this particular analogy. However, as an example of its use, assume there are two other propositions (one in the source and one in the target) in which 'heart' and 'observer' were in the agent place of a relation, and 'arrow' and 'radiant beauty' were in the object place, respectively. In such a case, those two propositions, and their relation, would be mapped because their constituents match those of the “C1=P1” node.
Step 8 is again not necessary to solve the Cupid analogy. However, if it were the case that there was no semantic similarity in this analogy, step 8 would provide possible mappings purely on the basis of structure (see section 5.5; Holyoak and Thagard, 1989).
4.2.2. Constructing Inhibitory Links. Once all of the plausible mappings and appropriate excitatory links have been constructed, it is necessary to identify conflicting mappings. Two mappings are considered to be conflicting if they map one element to two different elements. For example, if both the nodes “heart=observer” and “heart=sees” were validly constructed in the Cupid analogy, they would be considered to be in conflict because the concept 'heart' is being inconsistently mapped. It is very unlikely, though not impossible, that 'heart' will map to both 'observer' and 'sees' in a good analogy (Holyoak and Thagard, 1995). In order to capture this sense of "unlikeliness", inhibitory links are created in the mapping network between these conflicting mappings. The importance of these links becomes evident when the network is being settled, as they provide the means of competition among possible mappings (see section 4.3). In all of the example analogies run in Drama, these links are given the value of -0.2.
4.2.3. Constructing Pragmatic Links. Pragmatic links are simply excitatory links constructed on the basis of the importance of particular propositions to the solution of the analogy. The importance of a particular proposition is determined by its inclusion in a set of important propositions. In other words, Drama is simply told what is important. These links provide a means of capturing the pragmatic constraint of the multiconstraint theory (see section 2).
If it were the case that the agent who was mapping the Cupid analogy was particularly interested in the mapping of proposition C3, this proposition would be included in the set of important elements for the analogy. C3 would then play a greater role in driving the analogy, and mappings in which it plays a role would be more likely to be accepted.
4.3. Network Settling Algorithm
Once the mapping network has been constructed, it must be settled in order to determine the best mapping between source and target. The algorithm for settling the network considers the positive and negative constraints that were established during construction of the network and produces a globally optimal set of mappings. The procedure used for settling a network constructed by Drama is identical to that used to settle a network constructed by ACME. However, the networks themselves are different and thus the settling process produces different results (see section 6).
A cooperative network settling algorithm is used by Drama to solve the large constraint network, though it is only one of many suitable algorithms available for solving networks of this sort (Thagard and Verbeurgt, 1998). This particular algorithm has been chosen because of its psychological plausibility and general applicability to high-level reasoning (Rumelhart and McClelland, 1986; Holyoak and Thagard, 1989). A cooperative algorithm is, by definition, a parallel algorithm for satisfying interacting constraints. Thus, it is ideally suited to solving the network constructed in the previous steps of Drama. Hofstadter's Copycat model also uses a cooperative process for determining analogical mappings (see section 6.1).
The details of the algorithm used by Drama are not of great importance to determining the validity of Drama as a model of analogical mapping (see appendix C for a complexity analysis of the settling algorithm). Furthermore, our application is a simple implementation of a well-researched method of constraint satisfaction (Rumelhart, Smolensky et al., 1986). Thus, we will only provide a quick summary of the algorithm.
Each node in the network has its activation level updated on each cycle and in parallel. This update is based on the activation and link weights of connected nodes and given by the following equation:
aj(t+1)=aj(t)(1-d)+enetj(max-aj(t))+inetj(aj(t)-min)
Where aj(t) is the activation level of unit j at time t; d is the decay; min = -1; max = 1; enetj is the net excitatory input and inetj is the net inhibitory input both of which are given by Siwijoi(t) with the weight (link) wij>0 for enetj and wij<0 for inetj. The function oi(t) used to calculate enetj and inetj is max(aj(t), 0). Activation values of the nodes are constrained to be within (min, max).
This rule has been tested in comparison with other, similar rules and has been found to be flexible, accurate, and tractable (Holyoak and Thagard, 1989; Thagard forthcoming).
5. Applications of Drama
Like all high-level cognitive functions, analogizing has an extremely wide range of applications. Analogies are used to describe unfamiliar events in familiar terms, to explain poorly understood phenomena in terms of well understood ones, and to solve new problems by relating them to already solved problems. An instance of descriptive analogies is the Cupid example which describes the pangs of love in terms of the presumably more familiar physical pain. In the remainder of this section we examine a number of other, more complex analogies, each of which addresses an important aspect of human analogy-making.
In order to demonstrate the wide range of Drama's applicability, the values of all of the model's parameters have been kept unchanged between examples. Nevertheless, the representations on different runs of the same problems will vary because of our use of random concept vectors (see section 3). Though this variation provides some differences in activation values (i.e. levels of acceptance) of certain mappings, the reported results represent typical runs. From a psychological perspective, this variation among answers is one way in which Drama accounts for individual variations in providing analogical mappings.
5.1. Light bulb Analogy
A class of analogies that have been frequently discussed are the "convergence" analogies (Duncker, 1945; Gick and Holyoak, 1980; Gick and Holyoak, 1983; Holyoak and Thagard, 1989). In this class of analogies a source problem has been solved by having a number of weak forces converge on a central item to achieve the effect of a single large force without disturbing the item's surroundings. This solution is expected to be mapped to the target of the analogy. In our example, taken from Holyoak and Thagard (1989), the source problem is that of welding the filament of a light bulb without breaking the glass, and the target problem is to destroy a tumor without damaging the surrounding tissue. Tables 4 and 5 provide the input to Drama.
This introductory example should make clear the steps necessary to allow Drama to map a somewhat complex analogy. In this instance, the analogy is isomorphic, and not necessarily reliant on semantic information. In other words, a strictly syntactic mapping engine should be able to map this example correctly. This example also allows Drama to incorporate pragmatic information, since the problem has clearly defined goals (i.e. to destroy the tumor and not the surrounding tissue).
Table 4b
Semantic Input for the Lightbulb Analogy
|
Semantic Input for Lightbulb Analogy |
|
|
object = RandVec |
electromagnetic_wave = RandVec |
|
agent = RandVec |
light = electromagnetic_wave + RandVec |
|
rel = RandVec |
surround = RandVec |
|
not = RandVec |
outside = RandVec |
|
prop = RandVec |
laser = device + prop Ä beam + prop Ä light |
|
filament = RandVec |
high_beam = beam + prop Ä powerful |
|
bulb = RandVec |
low_beam = beam + prop Ä weak |
|
weak = RandVec |
not_fuse = not Ä fuse |
|
produce = RandVec |
not_destroy = not Ä destroy |
|
powerful = RandVec |
ray = beam + RandVec |
|
destroy = RandVec |
tissue = RandVec |
|
fuse = RandVec |
tumor = RandVec |
|
device = RandVec |
ray_source = device + prop Ä ray + prop Ä electromagnetic_wave |
|
beam = RandVec |
high_ray = ray + prop Ä powerful |
|
emits = RandVec |
low_ray = ray + prop Ä weak |
Table 5
Proposition Vector Input for the Lightbulb Analogy
|
Filament (Source) |
Tumor (Target) |
|
l1 = rel Ä surround + object Ä bulb + agent Ä filament |
r1 = rel Ä surround + object Ä tissue + agent Ä tumor |
|
l2 = rel Ä outside + object Ä laser + agent Ä bulb |
r2 = rel Ä outside + object Ä ray_source + agent Ä tissue |
|
l3 = rel Ä produce + object Ä laser + agent Ä high_beam |
r3 = rel Ä produce + object Ä ray_source + agent Ä high_ray |
|
l4 = rel Ä produce + object Ä laser + agent Ä low_beam |
r4 = rel Ä produce + object Ä ray_source + agent Ä low_ray |
|
l5 = rel Ä destroy + object Ä high_beam + agent Ä bulb |
r5 = rel Ä destroy + object Ä high_ray + agent Ä tumor |
|
l6 = rel Ä not_destroy + object Ä low_beam + agent Ä bulb |
r6 = rel Ä destroy + object Ä high_ray + agent Ä tissue |
|
l7 = rel Ä not_fuse + object Ä low_beam + agent Ä filament |
r7 = rel Ä not_destroy + object Ä low_ray + agent Ä tumor |
|
l8 = rel Ä not_destroy + object Ä bulb |
r8 = rel Ä not_destroy + object Ä low_ray + agent Ä tissue |
|
l9 = rel Ä fuse + object Ä laser + agent Ä filament |
r9 = rel Ä destroy + object Ä ray_source + agent Ä tumor |
|
|
r10 = rel Ä not_destroy + object Ä tissue |
Table 6 displays the answer provided by Drama. Accepted nodes are those which Drama has deemed the ‘best’ node to provide a particular mapping. A node is only considered to be a valid mapping if its final activation is above a threshold value of 0.2.
Table 6
Drama’s Solution to the Lightbulb Analogy
|
Accepted Mapping |
Activation |
|
ray_source = laser |
1.00000 |
|
surround = surround |
0.88261 |
|
tissue = bulb |
0.94852 |
|
tumor = filament |
0.94182 |
|
weak = weak |
0.94637 |
|
destroy = destroy |
0.61621 |
|
fuse = destroy |
0.46784 |
|
high_ray = high_beam |
0.81929 |
|
low_ray = low_beam |
0.81929 |
|
not_destroy = not_destroy |
0.39995 |
|
not_fuse = not_destroy |
0.57826 |
|
outside = outside |
0.84184 |
|
powerful = powerful |
0.94602 |
|
produce = produce |
0.92494 |
|
r1 = l1 |
0.86192 |
|
r10 = l8 |
0.88510 |
|
r2 = l2 |
0.86949 |
|
r3 = l3 |
0.88186 |
|
r4 = l4 |
0.88183 |
|
r6 = l5 |
0.82203 |
|
r7 = l7 |
0.84837 |
|
r8 = l6 |
0.55455 |
|
r9 = l9 |
0.78955 |
As table 6 shows, Drama maps the situation correctly. Drama has provided this correct answer despite having created a possible mapping network with 30% fewer nodes than that created by ACME for the same problem. Furthermore, this smaller network was created despite a 25% increase in mappable objects. This increase in objects was necessary to provide Drama with semantic information.
5.2. Animal Stories
Strong evidence for the psychological plausibility of Drama is provided through its application to a series of animal stories that were used to examine the abilities of children to perform analogical mappings (Gentner and Toupin, 1986). In total, eight different stories were used to determine the effects of systematicity and semantic similarity (referred to as transparency or surface similarity, by Gentner and Toupin) on analogical mapping in children. The source “dog story” for these analogies is presented in table 7. Tables 8 and 9 provide the input to Drama for the analogy between the “dog story” and the “cat story”.
Table 7c
The Source Story for the Animal Story Analogies
|
Animal Story Source |
|
The dog was strong. (Systematic version: The dog was jealous.) The dog was friends with a seal. The seal played with a penguin. The dog was angry. (Systematic version: Because the dog was jealous and the seal played with penguin, the dog was angry.)
The dog was reckless. (Systematic version: Because the dog was angry, it was reckless.) The dog got in danger. (Systematic version: Because the dog was reckless, it got in danger.) The penguin saved the dog. (Systematic version: Because the penguin saved the dog, the dog was friends with the penguin.) |
Table 8
Semantic Input for the Animal Stories
|
Semantic Input |
|
|
object = RandVec |
cause = RandVec |
|
agent = RandVec |
strong = RandVec |
|
rel = RandVec |
conjoin = RandVec |
|
prop = RandVec |
cat = animal + pet + RandVec |
|
animal = RandVec |
dog = animal + pet + RandVec |
|
ocean_goer = RandVec |
camel = animal + RandVec |
|
pet = RandVec |
seal = animal + ocean_goer + RandVec |
|
bird = RandVec |
walrus = animal + ocean_goer + RandVec |
|
friends = RandVec |
lion = animal + RandVec |
|
played = RandVec |
penguin = animal + bird + RandVec |
|
angry = RandVec |
seagull = animal + bird + RandVec |
|
reckless = RandVec |
giraffe = animal + RandVec |
|
endangered = RandVec |
theDog = dog + RandVec |
|
save = RandVec |
theCat = cat + RandVec |
|
jealous = RandVec |
|
The systematicity of the dog story is increased by including propositions relevant to the causes of events in the story; e.g. Because the dog was angry, it was reckless (see tables 7 and 9). The semantic similarity of the stories was altered by changing the similarity of the animals in the various roles (see table 8). Table 10 shows the set of semantic similarity conditions for the mappings. For example, in the S/D condition the target story is identical to that in table 7 except that the concept ‘dog’ is replaced by ‘seagull’, ‘seal’ by ‘cat’ and ‘penguin’ by ‘walrus’.
Table 9
Proposition Vector Input for the Systematic Dog/Cat Analogy
|
Dog Story (Source) |
Cat Story (Target) |
|
d1 = theDog + prop * jealous |
s1 = theCat + prop * jealous |
|
d2 = rel * friends + object * theDog + agent * seal |
s2 = rel * friends + object * theCat + agent * walrus |
|
d3 = rel * played + object * seal + agent * penguin |
s3 = rel * played + object * walrus + agent * seagull |
|
d4 = theDog + prop * angry |
s4 = theCat + prop * angry |
|
d5 = rel * conjoin + object * d1 + agent * d3 |
s5 = rel * conjoin + object * s1 + agent * s3 |
|
d6 = rel * cause + object * d5 + agent * d4 |
s6 = rel * cause + object * s5 + agent * s4 |
|
d7 = theDog + prop * reckless |
s7 = theCat + prop * reckless |
|
d8 = rel * cause + object * d4 + agent * d7 |
s8 = rel * cause + object * s4 + agent * s7 |
|
d9 = rel * endangered + object * theDog |
s9 = rel * endangered + object * theCat |
|
d10 = rel * cause + object * d7 + agent * d9 |
s10 = rel * cause + object * s7 + agent * s9 |
|
d11 = rel * save + object * penguin + agent * theDog |
s11 = rel * save + object * seagull + agent * theCat |
|
d12 = rel * friends + object * theDog + agent * penguin |
s12 = rel * friends + object * theCat + agent * seagull |
|
d13 = rel * cause + object * d11 + agent * d12 |
s13 = rel * cause + object * s11 + agent * s12 |
Table 10d
Semantic Similarity Conditions for Animal Story Analogies
|
Source |
Similar Objects/ Similar Roles (S/S) |
Dissimilar Objects (D) |
Similar Objects/ Dissimilar Roles (S/D) |
|
dog |
cat |
camel |
seagull |
|
seal |
walrus |
lion |
cat |
|
penguin |
seagull |
giraffe |
walrus |
Gentner and Toupin (1986) found that both systematicity and semantic similarity have effects on children's ability to provide appropriate analogies. They report that semantic similarity “strongly influenced” the ability to correctly perform the analogy; with less similar characters being more difficult to map. As well, for the older children systematicity greatly affected their ability to find the correct map; given a systematic story, 9 year olds could map it accurately regardless of semantic similarity. However, for younger children, systematicity did not seem to aid them in overcoming the difficulties associated with semantically similar concepts being used in different structural roles.
Table 11
Drama’s Performance with a Semantic Similarity Divisor of 10
|
Story |
Nodes |
Cycles |
Errors |
|
S Cat (S/S) |
188 |
26 |
0 |
|
S Camel (D) |
175 |
38 |
0 |
|
S Seagull (S/D) |
211 |
24 |
0 |
|
NS Cat (S/S) |
58 |
27 |
0 |
|
NS Camel (D) |
39 |
37 |
0 |
|
NS Seagull (S/D) |
54 |
59 |
3 |
Table 12
Drama’s Performance with a Semantic Similarity Divisor of 3
|
Story |
Nodes |
Cycles |
Errors |
|
S Cat (S/S) |
195 |
75 |
0 |
|
S Camel (D) |
185 |
75 |
2 |
|
S Seagull (S/D) |
199 |
75 |
5 |
|
NS Cat (S/S) |
54 |
29 |
1 |
|
NS Camel (D) |
47 |
39 |
2 |
|
NS Seagull (S/D) |
52 |
39 |
5 |
Tables 11 and 12 show Drama’s performance on these mapping problems. As figures 6 and 7 show, Drama performs very similarly to children on these problems.
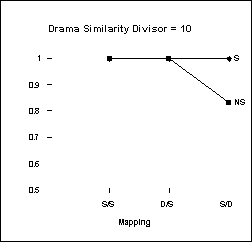
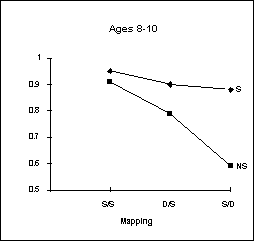
Figure 6. Drama’s performance compared to that of 8-10 year olds (adapted
from Gentner and Toupin, 1986).
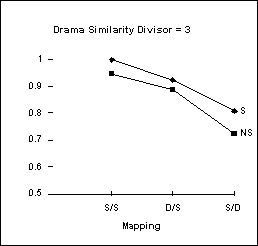

Figure
7. Drama’s performance compared
to that of 4-6 year olds (adapted from Gentner and Toupin, 1986).
Drama is able to capture the performance differences between age groups by varying its semantic similarity parameter (see figures 6 and 7). This parameter is used as a divisor on the similarity seed of nodes when they are created (see section 4.2.1). By decreasing this parameter from 10 (for 8-10 year olds) to 3 (for 4-6) year olds Drama effectively increases the importance of semantic similarity to the mapping process. In other words, by increasing the importance of semantics to such a high degree (i.e. to 3), the effects of extra structural information become minor (see figure 7). Thus, it seems likely that as children grow older, they place less importance on semantic similarity and pay more attention to the structure of a give situation in analogical mapping. This is equivalent to increasing the semantic similarity parameter in the Drama model.
5.3. Flow Analogy
The analogy between the flow of heat and the flow of water has been a standard test for computational models of analogy since its use by Gentner (1983). Both ACME and SME have been tested on this analogy and thus it will aid in comparing Drama to these two previous models (see section 6). In this analogy, the source situation is the well-understood occurrence of water flowing from one location to another due to a difference in pressure and the target is the less well-understood flow of heat caused by a difference in temperature.
Table 13 presents the encoding of the propositions which play a role in the analogy. Notably, much more information is known about the source than the target, as is often the case in such explanatory analogies. Also, the original encoding of this analogy by Falkenhainer, Forbus and Gentner (1986) was designed to include three impediments to constructing the proper analogy (Holyoak and Thagard, 1989). These are:
1. The concept 'clear' has no valid mapping.
2. Misleading semantic information concerning 'water' and 'coffee' both being liquids and having flat tops is included.
3. Irrelevant information concerning the diameters of the beaker and vial encourages an incorrect map of diameter to pressure instead of temperature to pressure.
Table 13
Proposition Vector Input for the Flow Analogy
|
Water Flow (Source) |
Heat Flow (Target) |
|
w1 = water + prop Ä flat_top |
h1 = coffee + prop Ä flat_top |
|
w2 = beaker + prop Ä clear |
h6 = rel Ä temperature + object Ä coffee + agent Ä val13 |
|
w3 = rel Ä diameter + object Ä beaker + agent Ä val1 |
h7 = rel Ä temperature + object Ä ice_cube + agent Ä val14 |
|
w4 = rel Ä diameter + object Ä vial + agent Ä val2 |
h8 = rel Ä greater + object Ä val13 + agent Ä val14 |
|
w5 = rel Ä greater + object Ä val1 + agent Ä val2 |
h9 = rel Ä flow + object Ä coffee + agent Ä ice_cube + stuff Ä heat + via Ä bar |
|
w6 = rel Ä pressure + object Ä beaker + agent Ä val3 |
h10 = rel Ä cause + object Ä h8 + agent Ä h9 |
|
w7 = rel Ä pressure + object Ä vial + agent Ä val4 |
|
|
w8 = rel Ä greater + object Ä val3 + agent Ä val4 |
|
|
w9 = rel Ä flow + object Ä beaker + agent Ä vial + stuff Ä water + via Ä pipe |
|
|
w10 = rel Ä cause + object Ä w8 + agent Ä w9 |
|
Table 14 shows the results from Drama's application to this analogy. Drama does not fall prey to any of these difficulties. Specifically, 'clear' is correctly mapped to nothing; 'water' and 'coffee' are not mapped, even though Drama relies on semantic information to drive much of its analogizing (see section 4.2.2); and the irrelevant information concerning diameters does not cause Drama to perform poorly. Most importantly, this example demonstrates that Drama has not sacrificed structural sensitivity in the name of semantics, but has rather successfully integrated both structure and semantics in its analogical mapping.
Table 14
Drama’s Solution to the Flow Analogy
|
Mapping |
Activation |
|
water = heat |
0.90252 |
|
temperature = pressure |
0.89613 |
|
pipe = bar |
0.90252 |
|
coffee = beaker |
0.93576 |
|
vial = ice_cube |
0.93576 |
|
cause = cause |
0.88264 |
|
flow = flow |
0.91925 |
|
greater = greater |
0.88069 |
|
flat_top = flat_top |
0.78194 |
|
val3 = val13 |
0.90541 |
|
val4 = val14 |
0.90541 |
|
w1 = h1 |
0.75434 |
|
w6 = h6 |
0.84530 |
|
w7 = h7 |
0.84530 |
|
w8 = h8 |
0.92373 |
|
w9 = h9 |
0.93585 |
|
w10 = h10 |
0.89258 |
This example also demonstrates an important difference in the theories underlying Drama and SME. In SME, this analogy is solved correctly essentially because there is built in preference for mappings which allow the most inferences. However, as Holyoak and Thagard (1989) have noted, this assumption has serious failings. It is a simple matter to construct an extended version of this example in which it is documented that the greater diameter of the beaker relative to the vial causes the beaker to have a greater volume. Also, in the heat flow situation, the volume of the coffee exceeds that of the ice cube. With this additional, irrelevant information, SME would be unable to determine if temperature should map to diameter or pressure. However, Drama, like ACME in this instance, relies on pragmatic information to guide the choice of mappings. It is assumed that the proposition concerning the cause of the flow of water is most important to the analogizer, as the analogizer is interested in explaining the flow of heat. With this natural assumption, Drama successfully solves the flow analogy in either case. Thus, any such irrelevant information does not adversely affect the mappings produced by Drama as it would for SME.
5.4. Missionaries Problem
In many instances, people can perform complex mappings in which more than one item in the source is mapped to one item in the target (many-to-one) or vice versa (one-to-many). An example which necessitates such mappings is the missionaries-and-cannibals problem (Gholson, Eymard et al., 1988). To solve the problem, it is necessary to get all of the missionaries across a river without any of them being eaten by the cannibals.
In order to solve this problem by analogy, the “farmer's dilemma” problem can be used as a source. The farmer's dilemma is to take a fox, a goose, and some corn across a mountain, without either the goose or the corn being eaten. Notably, the analogy between these two problems is not isomorphic, or one-to-one. Rather, all of the cannibals, or missionaries map equally well to either corn, fox or goose, so in the final answer we expect no particular missionary or cannibal to have a best mapping to its analog. Table 15 presents Drama's propositional input.
Table 15
Proposition Vector Input for the
Missionaries Analogy
|
Missionaries and Cannibals |
Farmer's Dilemma |
|
m1 = rel Ä carries + object Ä boat + agent Ä rower + agent2 Ä passenger |
f1 = rel Ä carries + object Ä wagon + agent Ä farmer + agent2 Ä thing |
|
m2 = rel Ä eat + agent Ä cannibal1 + object Ä missionary1 |
f2 = rel Ä eat + agent Ä fox + object Ä goose |
|
m3 = rel Ä eat + agent Ä cannibal1 + object Ä missionary2 |
f3 = rel Ä eat + agent Ä goose + object Ä corn |
|
m4 = rel Ä eat + agent Ä cannibal1 + object Ä missionary3 |
f4 = rel Ä cross_mountain + object Ä farmer |
|
m5 = rel Ä eat + agent Ä cannibal2 + object Ä missionary1 |
f5 = rel Ä cross_mountain + object Ä fox |
|
m6 = rel Ä eat + agent Ä cannibal2 + object Ä missionary2 |
f6 = rel Ä cross_mountain + object Ä goose |
|
m7 = rel Ä eat + agent Ä cannibal2 + object Ä missionary3 |
f7 = rel Ä cross_mountain + object Ä corn |
|
m8 = rel Ä cross_river + object Ä cannibal1 |
f8 = rel Ä not_eaten + object Ä corn |
|
m9 = rel Ä cross_river + object Ä cannibal2 |
f9 = rel Ä not_eaten + object Ä goose |
|
m10 = rel Ä cross_river + object Ä missionary1 |
|
|
m11 = rel Ä cross_river + object Ä missionary2 |
|
|
m12 = rel Ä cross_river + object Ä missionary3 |
|
|
m13 = rel Ä not_eaten + object Ä missionary1 |
|
|
m14 = rel Ä not_eaten + object Ä missionary2 |
|
|
m15 = rel Ä not_eaten + object Ä missionary3 |
|
Gholson et al. (1988) found that third and fourth grade children were able to use the farmer's dilemma as a source and transfer the solution to the missionaries problem. However, the converse was not true; i.e. the missionaries problem was not successfully used as a source. This has also been found to be the case for adults (Reed, Ernst et al., 1974). Gholson et al. suggest two possible explanations for this asymmetric transfer. The asymmetry may be due to “differences among the surface features of the problem” (i.e. semantics) or the asymmetrical transfer could be “related to the number of legal moves possible in each problem space” (Gholson, 1988, p. 51).
Table 16A
Drama’s Solution to the Missionaries Analogy with the Farmer’s Dilemma as Source
|
Mapping |
Activation |
|
carries = carries |
0.90077 |
|
rower = farmer |
0.87610 |
|
wagon = boat |
0.87610 |
|
eat = eat |
0.95610 |
|
not_eaten = not_eaten |
0.90419 |
|
thing = passenger |
0.87610 |
|
cross_river = cross_mountain |
0.91218 |
|
fox = cannibal2 |
0.48676 |
|
fox = cannibal1 |
0.39153 |
|
goose = cannibal2 |
0.26002 |
|
goose = cannibal1 |
0.30062 |
|
missionary1 = corn |
0.32359 |
|
missionary2 = corn |
0.58701 |
|
missionary3 = corn |
0.26435 |
|
missionary1 = goose |
0.30292 |
|
missionary2 = goose |
0.12319 |
|
missionary3 = goose |
0.37862 |
Table 16B
Drama’s Solution to the Missionaries Analogy with the Farmer’s Dilemma as Target
|
Mapping |
Activation |
|
carries = carries |
0.90077 |
|
rower = farmer |
0.87610 |
|
wagon = boat |
0.87610 |
|
eat = eat |
0.95636 |
|
not_eaten = not_eaten |
0.90384 |
|
thing = passenger |
0.87610 |
|
cross_river = cross_mountain |
0.90202 |
|
fox = cannibal1 |
0.50309 |
|
fox = cannibal2 |
0.35991 |
|
goose = cannibal1 |
0.25310 |
|
goose = cannibal2 |
0.34158 |
|
missionary1 = corn |
0.39149 |
|
missionary2 = corn |
0.53025 |
|
missionary3 = corn |
0.27297 |
|
missionary1 = goose |
0.25631 |
|
missionary2 = goose |
0.14303 |
|
missionary3 = goose |
0.36738 |
Which is a better explanation of asymmetrical mappings? We know that Drama effectively captures the effects of semantic information on mapping in children of the same age group tested by Gholson (see section 5.4). Furthermore, as tables 16A and 16B show, regardless which situation is a source or target, mapping of the analogy seems to take place equally well. Thus, the performance of Drama suggests that semantics alone will not account for this asymmetry. Gholson, et al.’s post hoc analysis similarly indicates that the number of solution paths is the more important property given these two alternatives.
Gholson, et al. suggest that any theory of analogical reasoning too dependent on structural information will be unable to explain these results:
This pattern of findings appears to have implications for theories of analogical reasoning based upon purely syntactic relations...This kind of approach suggests that transfer should be symmetrical in problems of the type used here (Winston, 1980, pp. 697-698). Our findings indicate that transfer is not symmetrical (Gholson, Eymard et al., 1988).
This realization prompts the authors to call for “research in which both surface and structural features are systematically manipulated” (ibid., 52). Though it does not provide an explanation of this asymmetry, Drama may help to indicate fruitful directions for further research.
5.5. Structure-only Analogy
Because most previous models of analogical mapping have been structure driven, and there is ample evidence to suggest structure is indeed important to this process (Gentner and Toupin, 1986; Falkenhainer, Forbus et al., 1989; Holyoak and Thagard, 1995), we anticipate some researchers may dismiss Drama because of its heavy reliance on semantic information. This final example concerns a simple analogy that contains no semantic information that is relevant to the final mapping. The input for this "boy/dog" analogy is presented in table 17.
Table 17
Proposition Vector Input for the Structure-only Analogy
|
Source |
Target |
|
f1 = bill + prop Ä smart |
s1 = rover + prop Ä hungry |
|
f2 = bill + prop Ä tall |
s2 = rover + prop Ä friendly |
|
f3 = steve + prop Ä smart |
s3 = fido + prop Ä hungry |
|
f4 = tom + prop Ä timid |
s4 = blackie + prop Ä frisky |
|
f5 = tom + prop Ä tall |
s5 = blackie + prop Ä friendly |
Drama's output is presented in table 18. The same solution is arrived at by a majority of human subjects who attempt the same problem (Holyoak and Thagard, 1989). How Drama is able to solve this semantically deficient analogy is basically by 'guessing'. Once Drama has attempted the analogy and been unable to construct any network based on semantic information, it simply assumes that structurally similar matches are possibly correct (see section 4). People seem to use a similar strategy in trying to solve this type of analogy (Keane, 1995).
Table 18
Drama’s Solution to the Structure-only Analogy
|
Accepted Mapping |
Activation |
|
s1 = f1 |
0.78332 |
|
s2 = f2 |
0.78122 |
|
s3 = f3 |
0.76499 |
|
s4 = f4 |
0.76084 |
|
s5 = f5 |
0.77494 |
|
rover = bill |
0.86825 |
|
smart = hungry |
0.86403 |
|
tall = friendly |
0.86790 |
|
steve = fido |
0.76395 |
|
tom = blackie |
0.86316 |
|
timid = frisky |
0.76087 |
Given this example, it is evident that Drama can perform structure-only analogies without necessitating a structure-only (or structure-mostly) mapping engine such as those used by ACME and SME. Once again, this example demonstrates that Drama provides an architecture which successfully amalgamates both structural and semantic constraints without sacrificing the strengths of either.
6. Evaluation of Drama
In the following sections, we examine Drama's neurological and psychological strengths and weaknesses with respect to ACME, SME and Copycat. This analysis allows us not only to contrast and compare Drama with ACME, SME and Copycat, it also highlights the ability of Drama to provide accounts of phenomena left unaddressed by its predecessors. This discussion demonstrates how Drama both incorporates and extends the scope of current computational models of analogy.
6.1. Neurological Plausibility
Drama's neurological plausibility is inherited from the neurological plausibility of distributed representations. However, the neurological plausibility of distributed representations is quite general. In other words, there is evidence that representations of this kind are used in the brain (Churchland and Sejnowski, 1992), but the precise nature of the representations is not understood (e.g., Are they HRRs? Are they tensor products? What dimensions do they represent? Are they encoding real values?, etc.). Furthermore, there is little specific data as to what neural structures are used in analogical reasoning, and Drama does not incorporate specific anatomical or physiological constraints. Nevertheless, using distributed representations makes Drama more neurologically plausible than predecessor models. Gentner and Markman (1993) have gone so far as to claim that analogy may be the Waterloo of distributed representations, suggesting that models with even Drama’s limited degree of neurological plausibility would not be forthcoming.
In the case of SME, standard symbolic representations are used. In both ACME and Copycat, however, connectionist ideas are incorporated to a degree. In particular, both models take advantage of parallel processing. However, both models use less neurologically plausible localist representations (Churchland and Sejnowski, 1992). Thus, both models rely on symbol manipulation to perform the analogical mapping process, whereas Drama manipulates vectors containing distributed representations. Mitchell (1993) expresses a desire to have Copycat achieve the level of neurological plausibility achieved by Drama (p. 226-7):
It may be that these (distributed) systems are more neurologically realistic than Copycat, but their distance from the cognitive level makes the problem of controlling their high-level behavior quite difficult... Ideally, a model should be constructed in which a structure such as Copycat’s Slipnet arises from such a low-level, distributed representation...but again the types of symbolic manipulations that have been achieved so far are not nearly complex enough to implement the types of processing performed by Copycat.
One property of Drama which is open to criticism as being neurologically unrealistic is its construction of localist representations for potential mappings in the mapping network. However, such a network could remain as a distributed HRR representation (see appendix B for an example). Notably, such an encoded network can be manipulated in its distributed form (Plate, 1994). These translations would likely not affect Drama's overall behavior, though this remains to be seen.
6.2. Psychological Plausibility
The HRRs used by Drama degrade, are subject to noise, and provide imperfect recall under certain circumstances, all of these properties are psychologically realistic. A number of other systems, including CADAM, CHARM, and TODAM2, use similar encoding schemes to provide convincing models of human memory access (Metcalfe Eich, 1985; Murdock, 1987; Plate, 1994).
Drama takes advantage of these properties through consistent encoding of conceptual information used in analogical mapping. Drama maintains concepts complex enough to query and to compare directly with one another to determine semantic similarity. For example, the concept ‘dog’ can be queried with: “What is a dog?” The program will respond “animal, animate, mammal, etc.”. Or it can be queried with: “Tell me about Fido.” The response will be “small, white, frisky, etc.” The first sort of query accesses the concept's isa relations and the second sort accesses properties of a particular dog. This sort of conceptual encoding allows for a large amount of semantic information to be available for use in the analogical mapping process. Furthermore, these encodings are used consistently in all of the example applications of Drama presented in this paper.
The psychological plausibility of the conceptual encoding used in Drama is made evident by the ability of the model to account for the effects of systematicity and semantic similarity in analogical mapping in children (see section 5.2). In this experiment, Drama was able to reproduce the interacting effects of semantic similarity and systematicity in its mapping of selected animal story analogs. In the same experiment, the semantic similarity system parameter provided an explanation for the variation in mapping abilities between age groups in mapping animal story analogies (see section 5.2). The ability of Drama to reproduce the behavior of two test groups across two interacting psychological variables with solely the variation of one system parameter is due to the interacting effects of semantics and structure in the model. Perhaps this example makes most clear the strengths of adopting the view that cognition is equally and concurrently sensitive to structure and semantics.
Though both the conclusion concerning asymmetrical mappings (section 5.4) and the account of the effects of systematicity in mapping provided by Drama are due to the importance of semantics to the model, we have not sacrificed generality to achieve these results. The performance of Drama on the structure-only analogy of section 5.5 shows its ability to handle semantically barren examples. Furthermore, misleading semantic information, such as that provided by Gentner for the flow analogy does not disrupt the model (see section 5.3). So, Drama has integrated semantics and structure in such a way that increases its psychological plausibility compared to current models, which we would expect given the claims of cognitive linguistics (Langacker, 1986).
Though Drama settles the potential mapping network in the same manner as ACME, the fact that it uses a different representational scheme, and a different method for constructing the mapping network serves to markedly improve its performance. Mitchell (1993) insists that ACME is a poor model of human analogy-making for four reasons:
1. ACME's method results in computationally infeasible and psychologically implausible mapping networks;
2. ACME's representations are rigid and hand tailored for each new analogy;
3. Semantics play a secondary role in the mapping process in ACME;
4. Concepts are devoid of depth, or richness.
Drama, however, is not subject to these criticisms. First, Drama's algorithms provide very different and generally much smaller mapping networks than those produced by ACME for the same problems (see table 19). The networks tend to be smaller because Drama uses the semantic information available to exclude highly improbably mappings that are considered by ACME. We have found no evidence that these smaller networks are less able to solve a given analogy.
Table 19
Comparison of Network Sizes for ACME and
Drama in Number of Unitse
|
Example |
ACME |
Drama |
|
Cannibals |
144 |
84 |
|
Heat Flow |
127 |
35 |
|
Laser Convergence |
192 |
117 |
|
Structure-only |
43 |
43 |
|
Non-systematic Animal |
125 |
~52 |
|
Systematic Animal |
214 |
~188 |
Second, Drama's representations are not ‘rigid’ representations. The precise representation used in an analogy may vary between runs. As well, Drama consistently uses an encoding scheme which captures aspects of human conceptual organization. Thus, Drama’s representations are not "hand-tailored" as Mitchell claims those of ACME are. However, the input itself is hand-tailored to some degree; the same degree as for any model of analogy handling equally complex real-world analogies. Third, semantics play a central role in Drama's recognition of potential mappings (see section 4). Lastly, the representations available to Drama are rich. The semantic structure of individual concepts can be captured through encoding both properties and isa relations. The animal stories examples in section 5.2 provides a simplified example of the conceptual richness available in any of Drama's analogies.
6.3. Shortcomings and Future Improvements
Though Drama has its limitations, these should be regarded in the context of other available models. In this context, we believe Drama is a significant improvement over current models as we have already shown. In this section we discuss the shortcomings of the model as well as improvements that are within the scope of the current model.
The ‘noisiness’ of HRRs has important consequences for its encoding and decoding accuracy. As noted in section 3, HRRs need to be 'cleaned up' in order to be recognized by the system (this occurs by finding the nearest known neighbor to a given decoded vector). This cleaning up process means that it is possible for a vector to be decoded incorrectly if the representation is noisy enough and the vector space is very crowded. Thus, the complexity of our conceptual space using HRRs is limited and proportional to the number of neurons being used to encode that space. Having to clean up each decoded vector by comparing it to every item in memory is a very expensive process. This is the means of clean up used in Drama, but is not the only available alternative. All that is necessary is for the clean up to either return a nearest neighbor (with the assumption that the neighbor is the ‘clean’ version of the given noisy vector) or to note that the noisy vector is not recognized. In the examples we ran, the number of stored vectors was small enough to perform this function exhaustively (i.e. comparing every item). With many more items in memory, special attention may have to be paid to precisely how this process is carried out, in order for it to be completed in a reasonable time and at a reasonable cost. It is not clear how different memory structures would affect the behavior of Drama. However, the general fact that the decoded vectors are noisy does not have an adverse affect on the behavior of Drama and may, in fact, provide more psychological realism than non-noisy representations.
As a psychological model, Drama’s shortcomings can be seen in its inability to account for asymmetry in the cannibals example, despite Drama’s theoretical commitments being appropriate ones for solving this problem (Gholson, et al., 1988). Furthermore, Drama cannot account for certain psychological data, such as the effects of the order in which propositions in an analogy are presented to a subject (Keane, 1995).
Of greater concern is the effect of the programmer’s choices on the representations used in analogical mapping. Though Drama generates (or could learn) the contents of HRRs, determining the set of propositions to be mapped necessitates the intervention of the programmer. However, this is the case for all current models of analogy.
A concern more specific to Drama, is that of incorporating distributed representations of the networks to be settled. Though Drama can clearly encode the structure of a generated mapping network, how the activations of network nodes and weights of links would be encoded and updated is not so easily resolved, though there are a number of options (see appendix B for further discussion).
Learning, which is an important part of repeated analogical mapping, is a multi-faceted problem. As noted, learning representation contents could be naturally included in a distributed model like Drama (section 3). However, the ability to learn common mappings, and re-representation of certain structures to aid complex mappings, is not as straightforward a problem. Increasing saliency of elements in a structure is possible with HRRs,[4] and increasing familiarity could be accomplished through minor architectural changes. In particular, rather than having a single large memory for all vectors, we could identify multiple types of memory, such as short term memory and working memory which would hold only certain vectors, depending on their relevance to the current mapping problem and past mappings. However, the details of these architectural changes need to be worked out and may adversely effect the current performance of the model.
Unlike these more difficult changes, we feel Drama needs only minor modification to account for the other two steps in analogical reasoning; application, and retrieval. Consider first the application stage of analogical reasoning (section 2), which includes behaviors such as candidate inference and schema generation. Schema generation could be accomplished by binding a superposition of example role fillers (i.e. the fillers in the target and source) into that same role in the schema. The result would be a schema with the same structure, but with combined (in a sense generalized) semantics, as one would expect. Furthermore, the type of encoding used in Drama has been shown to facilitate queried analogies of the sort: “mother is to baby as mare is to what?” These A:B::C:? analogies which have been modeled using tensor products by Halford, et al. (1994) could be encoded into Drama-like representations. In fact, by introducing an "unknown" element into the examples, the results of mapping that element can be interpreted as an inference to the value of the unknown element. This procedure has been used in ACME to perform inference and would transfer neatly to Drama since many of their mapping results agree. However, ACME is often overly powerful at such inference. Using the semantic information available in Drama to limit acceptable inferences would likely lead to more plausible results.
Perhaps the most obvious extension to Drama is an account of retrieval (see section 3). Plate (1994) provides a discussion of the ability of HRRs to capture both structure and semantics in a single vector. This makes it extremely easy to find similar vectors, and thus analogical sources, in very large memories. Once a number of sources have been recalled, comparative mappings could be performed using the current version of Drama. Plate (forthcoming) provides a detailed discussion of the degree to which structure is preserved in HRR encodings. From his results, it seems that the retrieval process can be performed efficiently and effectively. The possible source analogies retrieved could then be used directly by Drama.
7. Distributed Models of Analogy
There are currently few distributed models of analogy, as methods for encoding structure in distributed representations have become available only recently. To the best of our knowledge, Drama is the only conjunctive coding (i.e. HRR, tensor product, etc.) model of analogical mapping that handles cases more complex than simple single proposition A:B::C:D analogies (Halford, Wilson et al., 1994). However, another model, LISA (Learning and Inference with Schemas and Analogies), also claims to be a distributed model of analogy and uses dynamic binding instead of conjunctive coding (Hummel, 1994; Hummel and Holyoak, 1997).
LISA has been successful in solving simple analogies and future versions of this model may well solve models as complex as those presented in this paper. Like Drama, LISA is semantically driven, stochastic, and reliant on connectionist principles for implementation. However, there are a number of important differences between LISA and Drama.
The first difference is that, because of inherent limitations of the LISA architecture, it is far from clear that the model will be able to handle sufficiently complex analogies. The two most evident limitations of LISA are that it is only able to store one proposition in working memory at a time, and that it can only represent one structural level at a time. These limitations suggest that LISA would not be able to handle examples such as the flow analogy (section 5.3), because there is no mechanism that would allow a distinction between the pressure-temperature mapping and the diameter-temperature mapping. In other words, LISA would have no way to compare these two mappings as there would be no "memory" of one mapping while the other was being evaluated since only one proposition can be in working memory at a time.
Furthermore, with only one structural level available in working memory at a time, there does not appear to be a way for LISA to distinguish between two of the same second-order propositions in one "story". For example, if there were two causal relations with propositions in each place in a target, LISA would not be able to distinguish them in their mappings to a source with two similar causal relations. Since semantic and structural information for the "next level down" can not be brought to bear on the problem (i.e. loaded into working memory), LISA would not be able to make the appropriate distinctions between mappings and could not determine the best mapping. Therefore, LISA could not solve the extended version of the heat flow/water flow analogy discussed at the end of section 5.3.
These same limitations provide LISA with a distinct advantage over Drama. It is undeniable that there are limitations on the capacity of human working memory (Miller, 1956; Halford et al., 1994). Currently, Drama does not sufficiently account for these limitations, though there is a limitation on the size of the conceptual memory in the Drama model. However, it is far from clear that LISA has done a satisfactory job in accounting for these limitations either. As noted, LISA seems to be more limited in its capacity to perform analogical mappings than humans. Neither Drama nor LISA are clearly better when it comes to modeling this aspect of human performance.
Aside from these implementation difficulties, there are problems with theoretical commitments implemented in LISA. Though Hummel and Holyoak (1997) claim that LISA is a distributed model, it is only partially so. Only low-level semantic information is encoded in a distributed manner. The structural relations amongst components of propositions are encoded using purely localist methods. There are units dedicated to entire propositions, as well as each sub-part of the proposition. This form of encoding is highly unrealistic (Churchland and Sejnowski, 1992). Drama, in contrast, encodes all structural and semantic information in the same way, using distributed representations.
Furthermore, semantic information encoded in LISA relies on “semantic primitives” that are defined based on the intuitions of the researcher (Hummel, personal communication). Though this is not an uncommon approach to encoding such information, HRRs do not have to rely on such intuition. HRRs could be encoded directly from environmental input although in Drama they are random (which is still independent of the researcher). Intuiting which semantic information is to be explicitly encoded leads to inconsistencies in the input used for LISA. In one example, the property of a beam being "strong" is encoded as distributed semantic information. In a different example, the property of a person being "smart" is encoded through localist structural information. How one makes such a distinction between two properties, both of which play identical roles, seems to be a matter of convenience. In other words, the encoding of a particular problem seems dependent on what LISA "needs to know" to solve that problem. Furthermore, LISA encodes all types of semantic information in the same way, with no distinction between 'isa' relations and properties. In contrast, Drama consistently accepts properties as encoded as 'prop Ä <property>' and distinguishes these from 'isa' relations which are encoded solely as superpositions.
On the more neurological side, LISA has a strong commitment to synchrony binding as a means of encoding structural relations. Though there are a number of connectionist models which use synchrony binding, the neurological evidence for this sort of mechanism is controvertible (Hardcastle, 1997). Recent psychophysical experiments by Kiper, et al. (1996) have shown that the physiologically observed oscillatory responses in the human brain are unrelated to the processes underlying visual segmentation and perceptual grouping. It is these exact responses that are often used as a basis for justifying a commitment to neural synchrony as a means of solving the perceptual binding problem (Gray and Singer, 1989; von der Malsburg, 1983; Singer, 1991). LISA uses synchrony binding in a similar way to capture the structure of propositions. So, it seems that Kiper, et al.'s results lessen the neurological plausibility of LISA. Furthermore, synchrony binding models tend to share a commitment to localist encodings in order to facilitate binding by neural synchrony (Shastri and Ajjanagadde, 1993; Park and Robertson, 1995). In general, then, it is not at all clear that a completely distributed model could be forthcoming with a commitment to synchrony as found in LISA.
8. Conclusions
Drama is an improvement over currently available models of analogical mapping in terms of both neurological and psychological plausibility. The numerous examples in this paper provide ample evidence of the ability of Drama to provide a distributed account of structurally complex tasks. In other words, Drama has successfully applied connectionist ideas to a high-level cognitive task, undermining the claims by Fodor and Pylyshyn (1988), Fodor and McLaughlin (1989), and others that distributed representations are not able to provide good models of cognitive tasks more obviously suited to symbolic representations.
Drama is able to both account for and extend the successes of its predecessor models SME, ACME, and Copycat. Compared to LISA, Drama is more faithful to the commitments of distributed computation and representation, and is likely more neurologically realistic. Most notably, Drama is able to successfully model the developmental changes in analogical performance on the basis of a decrease in the importance of similarity as children grow older. This kind of result lends support to the theoretical commitment of Drama to integrate structure and similarity. Without such a commitment, we feel it is unlikely that Drama would be as successful in modeling such a wide variety of analogical phenomena.
9. References
Abbott, L. F. (1994). Decoding neuronal firing
and modeling neural networks. Quarterly
Review of Biophysics 27(3):
291-331.
Barnden, J.A. (1994). On using analogy to
reconcile connections and symbols. In D.S. Levine & M. Aparicio (Eds.), Neural networks for knowledge representation
and inference, pp.27-64. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Bechtel, W. (1995). Connectionism. In S. Guttenplan (Ed.), A companion to the philosophy of mind. Cambridge, MA: Blackwell.
Bechtel, W. and R. C. Richardson (1993). Discovering complexity: decomposition and localization as strategies in scientific research. Princeton, NJ, Princeton University Press.
Borsellino, A. and T. Poggio (1973). Convolution and correlation algebras. Kybernetik, 13, 113-122.
Churchland, P. (1989). A neurocomputational perspective. Cambridge, MA: MIT Press.
Churchland, P. M. (1992). A feed-forward network for fast stereo vision with a movable fusion plane. In K. Ford and C. Glymour (Eds.), Android Epistemology: Proceedings of the 2nd International Workshop on Human and Machine Cognition, Cambridge, MA: AAAI Press/MIT Press.
Churchland, P. M. (1995). Machine stereopsis: A feedforward network for fast stereo vision with movable fusion plane. In K. Ford, C. Glymour, and P. Hayes (Eds.), Android Epistemology. Menlo Park: MIT Press.
Churchland, P. S. and T. Sejnowski (1992). The computational brain. Cambridge, MA: MIT Press.
Clark, A. and J. Toribio (1994). “Doing without representing?” Sythese. 101: 401-431.
Duncker, K. (1945). On problem solving. Psychological Monographs, 58, no. 270.
Eskridge, T. C. (1994). A hybrid model of continuous analogical reasoning. Advances in connectionist and neural computation theory: Analogical connections. Norwood, NJ: Ablex.
Falkenhainer, B., K. D. Forbus, and D. Gentner (1989). The structure-mapping engine: Algorithms and examples. Artificial Intelligence, 41, 1-63.
Feige, U. and M. X. Goemans (1995). Approximating the value of two prover proof systems, with applications to MAX 2SAT and MAX DICUT. Proceedings of the Third Israel Symposium on Theory of Computing and Systems, Tel Aviv, Israel, p. 182-189.
Fodor, J. and B. McLaughlin (1990). Connectionism and the problem of systematicity: Why Smolensky’s solution doesn’t work. Cognition, 35, 183-204.
Fodor, J. and Z. Pylyshyn (1988). Connectionism and cognitive architecture: A critical analysis. Cognition, 28, 3-71.
Gentner (1983). Structure-mapping: A theoretical framework for analogy. Cognitive Science. 7(2): 155-170.
Gentner, D. and K. Forbus (1991). MAC/FAC: A model of similarity-based retrieval. Proceedings of the Thirteenth Annual Conference of the Cognitive Science Society. Hillsdale, NJ: Erlbaum.
Gentner, D. and A. B. Markman (1993). Analogy - watershed or Waterloo? Structural alignment and the development of connectionist models of analogy. In C. L. Giles, S. J. Hanson and J.D. Cowan (Eds.), Advances in neural information processing systems - 5. San Mateo, CA: Morgan Kaufmann.
Gentner, D. and C. Toupin (1986). Systematicity and surface similarity in the development of analogy. Cognitive Science, 10, 277-300.
Gholson, B., L. A. Eymard, D. Long, D. Morga, and F.C. Leeming (1988). Problem solving, recall, isomorphic transfer, and non-isomorphic transfer among third-grade and fourth-grade children. Cognitive Development, 3, 37-53.
Gick, M. L. and K. J. Holyoak (1980). Analogical problem solving. Cognitive Psychology, 12, 306-355.
Gick, M. L. and K. J. Holyoak (1983). Schema induction and analogical transfer. Cognitive Psychology, 15, 1-38.
Gorman, R. P. and T. J. Sejnowski (1988). Analysis of hidden units in a layered network trained to classify sonar targets. Neural Networks, 1, 75-89.
Gray, C. and W. Singer (1989). Stimulus-specific neuronal oscillations in orientation-specific columns of the visual cortex. PNAS, 86, 1689-1702.
Halford, G. S., W. H. Wilson, J. Guo, R.W. Gayler, G. Wiles, and J.E.M. Stewart (1994). Connectionist implications for processing capacity limitations in analogies. Advances in connectionist and neural computation theory, Vol. 2: Analogical connections. Norwood, NJ: Ablex.
Hall, R. (1989). Computational approaches to analogical reasoning: A comparative analysis. Artificial Intelligence, 39, 39-120.
Harnad, S. (1992). Connecting object to symbol in modeling cognition. In A. Clark and R. Lutz (Eds.), Connectionism in Context. London, Springer-Verlag.
Hardcastle, V. (1997). Consciousness and the neurobiology of perceptual binding. Seminars in Neuroscience, 17(2), 163-170.
Hinton, G. E. (1986). Learning distributed representations of concepts. Eighth Conference of the Cognitive Science Society, Lawrence Erlbaum Associates.
Hofstadter, D. (1995). A review of mental leaps: analogy in creative thought. , 16, 75-80.
Hofstadter, D. R. and M. Mitchell (1988). Conceptual slippage and mapping: A report of the Copycat project. Proceedings of the Tenth Annual Conference of the Cognitive Science Society. Hillsdale, New Jersey: Erlbaum.
Holyoak, K. and P. Thagard (1995). Mental leaps: Analogy in creative thought. Cambridge, MA: MIT Press.
Holyoak, K. J. and P. Thagard (1989). Analogical mapping by constraint satisfaction. Cognitive Science, 13, 295-355.
Hummel, J. E., B. Burns, and K.J. Holyoak (1994). Analogical mapping by dynamic binding: Preliminary investigations. Advances in connectionist and neural computation theory: Analogical connections. Norwood, NJ: Ablex.
Hummel, J. E. and K. J. Holyoak (1997). Distributed representations of structure: a theory of analogical access and mapping. Psychology Review, 104(3), 427-66.
Keane, M. T. (1995). On order effects in analogical mapping: Predicting human error using IAM. In J. D. Moore, J.F. Lehman (Eds.), Seventeenth Annual Conference of the Cognitive Science Society, Hillsdale, NJ: Erlbaum.
Kedar-Cabelli, S. (1988). Analogy - From a unified perspective. In Helman, D. Analogical reasoning. Netherlands: Kluwer.
Kiper, D., R. Karl, J. Movshon. (1996). Cortical oscillatory responses do not affect visual segmentation. Vision Research, 36(4), 539-544.
Kosslyn, S. (1994). Image and brain: The resolution of the imagery debate. Cambridge, MA: MIT Press.
Langacker, R.W. (1986), An Introduction to Cognitive Grammar, Cognitive Science, 10, 1-40.
Langacker, R. W. (1987). Foundations of cognitive grammar. Stanford: Stanford University Press.
Lazzaro, J. and C. Mead (1989). A silicon model of auditory localization. Neural Computation, 1, 47-57.
Le Cun, Y., B. Boser, J. Denker, D. Henderson, R. Howard, W. Hubbard, and L. Jackel (1990). Handwritten digit recognition with a back-propagation network. In D. Touretzky (Ed.), Advances in neural information processing systems - 2. San Mateo: Morgan Kaufmann.
Legendre, G., Y. Miyata, and P. Smolensky (1994). Principles for an integrated connectionist/symbolic theory of higher cognition. Hillsdale, NJ: Lawrence Erlbaum Associates.
Metcalfe Eich, J. (1985) Levels of processing, encoding specificity, elaboration and CHARM. Psychological Review, 92(1): 1-38.
Miikkulainen, R. and M. G. Dyer (1988). Encoding input/output representations in connectionist cognitive systems. In D. Touretsky, G. Hinton and T. Sejnowski (Eds.), Connectionist Models Summer School, San Mateo: Morgan Kaufmann Publishers.
Mitchell, M. (1993). Analogy-making as perception. Cambridge, MA: MIT Press.
Murdock, B. B. (1987). Serial-order effects in a distributed-memory model. In Gorfein, D. S. and Homan,R. R. (Eds.), Memory and Learning: The Ebbinghaus Centennial Conference. Lawrence Erlbaum Associates.
Park, N. S. and D. Robertson (1995). A localist network architecture for logical inference based on temporal synchrony approach to dynamic variable binding. The IJCAI workshop on Connectionist-Symbolic Integration.
Plate, T. A. (1993). Holographic recurrent networks. In C. L. Giles, S. J. Hanson and J.D. Cowan (Eds.), Advances in neural information processing systems - 5. San Mateo, Morgan Kaufmann.
Plate, T. A. (1994). Distributed representations and nested compositional structure. Ph.D. Thesis, Toronto: University of Toronto.
Plate, T. A. (forthcoming). Estimating analogical similarity by vector dot products of Holographically Reduced Representations. Cognitive Science.
Qian, N. and T. J. Sejnowski (1988). Learning to solve random-dot stereograms of dense and transparent surfaces with recurrent backpropagation. In D. Touretsky, G. Hinton and T. Sejnowski (Eds.), Connectionist Models Summer School, San Mateo: Morgan Kaufmann Publishers.
Raeburn, P. (1993). Reverse engineering the human brain. Technology Review. November.
Reed, S. K., G. W. Ernst, and R. Banerji (1974). The role of analogy in transfer between similar problem states. Cognitive Psychology , 6, 436-440.
Rumelhart, D., P. Smolensky, G. Hinton, and J. McClelland (1986). Schemata and sequential thought processes in PDP models. In D.E. Rumelhart and J. L. McClelland (Eds.), Parallel distributed processing: Explorations in the microstructure of cognition. Cambridge MA: MIT Press/Bradford Books.
Rumelhart, D. E. and J. L. McClelland, Eds. (1986). Parallel distributed processing: Explorations in the microstructure of cognition. Cambridge MA: MIT Press/Bradford Books.
Sarle, W. S. (1994). Neural networks and statistical models. 19th Annual SAS Users Group International Conference.
Shastri, L. and V. Ajjanagadde (1993). From simple associations to systematic reasoning: A connectionist representation of rules, variables, and dynamic bindings. Behavioral and Brain Sciences, 16, 417-94.
Singer, W. (1991). The formation of cooperative cell assemblies in the visual cortex. In J. Kruger (Ed.), Neuronal cooperativity. Berlin: Springer.
Skarda, C. A. and W. J. Freeman (1987). How brains make chaos in order to make sense of the world. Behavioral and Brain Sciences, 10, 161-195.
Smolensky, P. (1988). On the proper treatment of connectionism. Behavioral and Brain Sciences, 11(1), 1-23.
Smolensky, P. (1990). Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artificial Intelligence. 46, 159-217.
Smolensky, P. (1995). Computational models of mind. A companion to the philosophy of mind. Cambridge, MA: Blackwell.
Thagard, P. (forthcoming). Computing Coherence. Cognitive Models of Science, Minnesota Studies in the Philosophy of Science. Minneapolis: University of Minnesota Press.
Thagard, P., K. Holyoak, G. Nelson, and D. Gochfeld (1990). Analog retrieval by constraint satisfaction. Artificial Intelligence, 46, 259-310.
Thagard, P. and K. Verbeurgt (1998). Coherence as constraint satisfaction. Cognitive Science. 22.
Tomasello, M., Ed. (1998). The new psychology of language: Cognitive and functional approaches to language structure. London, L. Erlbaum Associates.
Ungerer, F. and H.
Schmid (1996). An introduction to
cognitive linguistics, Addison-Wesley.
von der Malsburg, C. (1983). How are
nervous systems organized? In E. Basar, H. Flohr, H. Haken and A. J. Mandell
(Eds.), Synergetics of the brain. Berlin: Springer.
Appendix A
The Details of HRR Operations
Consider a set E of elements which are holographic reduced representations (HRRs). A member of E is an n-dimensional vector whose contents may represent an image, a proposition, a concept, etc. The prima facie similarity of two vectors is captured by their dot product. The operations necessary to encode and decode HRRs can be understood as follows:
Let ![]() be the space of item
vectors in n-dimensions, and let
be the space of item
vectors in n-dimensions, and let ![]() be the space of
stored vectors in n-dimensions.
be the space of
stored vectors in n-dimensions.
Let
![]()
be the encoding operation (circular convolution),
![]()
be the decoding operation (circular correlation), and
![]()
be the superposition operation (addition). These three operations make it possible to store any relations necessary for generating the network of relations amongst elements of E.
More precisely, the circular convolution operation Ä is often referred to simply as convolution and consists of the following operations for c = a Ä b where a, b, and c are n-dimensional vectors:
co = aobo + anb1 + an-1b2 + ... + a1bn
c1 = an-1bo + an-2b1 + ... + anbn
M
cn = anbo + an-1b1 + ... + aobn
or
![]() for j=0 to n-1 (subscripts are modulo-n)
for j=0 to n-1 (subscripts are modulo-n)
This operation can be represented as:

Figure 8. Visual representation of circular convolution (adapted from Plate (1994)).
Similarly, the circular correlation operation # is often referred to simply as correlation and consists of the following operations for d = a # c:
do = aoco + a1c1 + ... + ancn
d1 = anco + aoc1 + ... + an-1cn
M
dn = a1co + anc1 + ... + aocn
or
![]() for j=0 to n-1 (subscripts are modulo-n)
for j=0 to n-1 (subscripts are modulo-n)
This operation can be represented as:
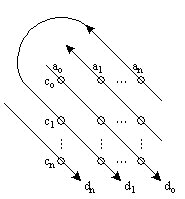
Figure 9. Visual representation of circular correlation (adapted from Plate (1994)).
Notably, the correlation of two vectors a # c can be written as a* Ä c where a* is the approximate inverse of a which is defined as:
Let
a = {ao, a1, ..., an}
then
a* = {ao, an, ..., a1}
Though the exact inverse, a-1, could be used to decode a Ä c exactly, this process results in a lower signal-to-noise ratio in the retrieved vectors in most instances.
Appendix B
Example Encoding of a Settling Network
Table 20 summarizes the encoding of the settling network for the Cupid analogy presented in section 4. In order to encode a settling network, it is necessary to introduce the relationship ‘maps’ and the operators ‘excite’ and ‘inhibit’. Notably, the example analogy does not have any inhibitory links, but they would be encoded in the same manner as the excitatory links.
Table 20
Example Encoding of a Settling Network
|
Node Encoding |
|
N1=rel Ä maps + object Ä C3 + agent Ä P3 + excite Ä N2 + excite Ä N3 + excite Ä N4 |
|
N2=rel Ä maps + object Ä C1 + agent Ä P1 + excite Ä N1 + excite Ä N3 + excite Ä N4 + excite Ä N5 + excite Ä N6 + excite Ä N7 |
|
N3=rel Ä maps + object Ä C2 + agent Ä P2 + excite Ä N1 + excite Ä N2 + excite Ä N4 + excite Ä N8 |
|
N4=rel Ä maps + object Ä cause + agent Ä cause + excite Ä N1 + excite Ä N2 + excite Ä N3 |
|
N5=rel Ä maps + object Ä feels + agent Ä sees + excite Ä N2 + excite Ä N6 + excite Ä N7 |
|
N6=rel Ä maps + object Ä heart + agent Ä observer + excite Ä N2 + excite Ä N5 + excite Ä N7 |
|
N7=rel Ä maps + object Ä arrow + agent Ä beauty + excite Ä N2 + excite Ä N5 + excite Ä N6 |
|
N8=rel Ä maps + object Ä pang + agent Ä hurts + excite Ä N3 |
In addition to the encoded network presented in table 20 it is necessary to encode the excitation or inhibition weights and the current activation of each node. There are a number of options for doing this. It could be supposed that a separate vector of current activations and weights was maintained, or that an activation operator could be defined and attached to each node. In the latter case, the activation vector would be interpreted differently than a standard vector, i.e. as encoding a value rather than a position in concept space (Abbott, 1994). In the case of weights, this sort of encoding could be used as one element in the two place relations ‘excite’ or ‘inhibit’. It is important to note that the network settling could take place in the encoded form. HRRs need not be decoded in order to perform structural manipulation (see Plate, 1994).
Unfortunately, using encoded settling networks greatly increases the execution time of network construction on a serial computer. Network construction would be slowed for two reasons. First, the dimensionality of the concept space would have to be increased to allow accurate decoding in light of the additional vectors needed to encode the network. This increase in dimensionality would slow the network construction. Second, a minimal increase in time would come from the encoding process itself when constructing the nodes. Because run times of the current analogies are on the order of days, it is not currently feasible to use encoded networks in our examples. This extension could be feasible on faster hardware or, preferably, through a parallel implementation.
Appendix C
Complexity Analysis of the Worst Case
The length of time needed to construct a network using the algorithm presented in section 4 varies as a function of the number of vectors in memory (V) and the dimensionality of each vector (N). The most important operations for constructing the network are the dot product, which is O(N) and the decode operation which consists in V dot product operations and is thus O(NV). Proceeding through the algorithm step by step, we find the following:
Step 1: We need to perform V2 dot products – O(NV2).
Step 2: We need to compare all results to a threshold and in the worst case construct V2 nodes – O(V2).
Step 3: We must perform a decode operation, O(NV), for each of V2 nodes – O(NV3).
Steps 4 and 5: These link constructions are on the order of V – O(V).
Step 6: Like the link steps, this step is dependent on the maximal number of constituents in any proposition which must be less than V. Thus, the size of the network cannot be greater than V2 – O(V2).
Steps 7 and 8: These steps do not occur in the worst case. When they do occur, their complexity is much less than that of step 3.
Given this analysis, it is clear that step 3 determines the order of the algorithm, which is O(NV3).
Of course, this analysis is for the complexity on a serial computer and does not reflect the length of time of execution on a parallel machine. Most importantly, both the dot product and the decode operation can be done in a single step on a parallel machine. Thus, the high complexity does not reflect negatively on the algorithm in a neurological context.
The problem of network settling is known to be NP-hard (Thagard and Verbeurgt 1998). However, similar problems can be closely approximated (.878) with polynomial time algorithms (Feige and Goemans 1995). All of our examples settled quickly and scale about linearly with the network size (For a more in-depth treatment of the computational properties of settling the networks and a characterization of the functions being minimized see Thagard and Verbeurgt (1998)).